
【题目】如图1,A、B、C、D为矩形的四个顶点,AD=4cm,AB=dcm.动点E、F分别从点D、B出发,点E以1cm/s的速度沿边DA向点A移动,点F以1cm/s的速度沿边BC向点C移动,点F移动到点C时,两点同时停止移动.以EF为边作正方形EFGH,点F出发xs时,正方形EFGH的面积为ycm2 . 已知y与x的函数图象是抛物线的一部分,如图2所示.请根据图中信息,解答下列问题:
(1)自变量x的取值范围是;
(2)d= , m= , n=;
(3)F出发多少秒时,正方形EFGH的面积为16cm2?
【答案】
(1)0≤x≤4
(2)3;2;25
(3)
解:如图,过点E作EI⊥BC垂足为点I.则四边形DEIC为矩形,
∴EI=DC=3,CI=DE=x,
∵BF=x,
∴IF=4﹣2x,
在Rt△EFI中,EF2=EI2+IF2=32+(4﹣2x)2,
∵y是以EF为边长的正方形EFGH的面积,
∴y=32+(4﹣2x)2,
当y=16时,32+(4﹣2x)2=16,
整理得,4x2﹣16x+9=0,
解得,x1= ![]() ,x2=
,x2= ![]() ,
,
∵点F的速度是1cm/s,
∴F出发 ![]() 或
或 ![]() 秒时,正方形EFGH的面积为16cm2.
秒时,正方形EFGH的面积为16cm2.

【解析】解:(1)∵BC=AD=4,4÷1=4,
∴0≤x≤4;
所以答案是:0≤x≤4;(2)根据题意,当点E、F分别运动到AD、BC的中点时,
EF=AB最小,所以正方形EFGH的面积最小,
此时,d2=9,m=4÷2=2,
所以,d=3,
根据勾股定理,n=BD2=AD2+AB2=42+32=25,
所以答案是:3,2,25;
【考点精析】通过灵活运用勾股定理的概念,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.


科目:初中数学 来源: 题型:
【题目】某校九年级有24个班,共1000名学生,他们参加了一次数学测试,学校统计了所有学生的成绩,得到下列统计图.
(1)求该校九年级学生本次数学测试成绩的平均数;
(2)下列关于本次数学测试说法正确的是( )
A.九年级学生成绩的众数与平均数相等
B.九年级学生成绩的中位数与平均数相等
C.随机抽取一个班,该班学生成绩的平均数等于九年级学生成绩的平均数
D.随机抽取300名学生,可以用他们成绩的平均数估计九年级学生成绩的平均数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2﹣4a(a>0)与x轴相交于A,B两点(点A在点B的左侧),点P是抛物线上一点,且PB=AB,∠PBA=120°,如图所示.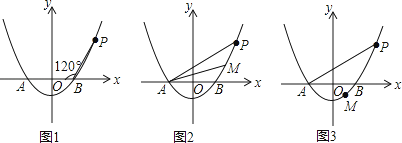
(1)求抛物线的解析式.
(2)设点M(m,n)为抛物线上的一个动点,且在曲线PA上移动.
①当点M在曲线PB之间(含端点)移动时,是否存在点M使△APM的面积为 ![]() ?若存在,求点M的坐标;若不存在,请说明理由.
?若存在,求点M的坐标;若不存在,请说明理由.
②当点M在曲线BA之间(含端点)移动时,求|m|+|n|的最大值及取得最大值时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,地面上两个村庄C、D处于同一水平线上,一飞行器在空中以6千米/小时的速度沿MN方向水平飞行,航线MN与C、D在同一铅直平面内.当该飞行器飞行至村庄C的正上方A处时,测得∠NAD=60°;该飞行器从A处飞行40分钟至B处时,测得∠ABD=75°.求村庄C、D间的距离( ![]() 取1.73,结果精确到0.1千米).
取1.73,结果精确到0.1千米).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2011年徐州市全年实现地区生产总值3551.65亿元,按可比价格计算,比上年增长13.5%,经济平稳较快增长.其中,第一产业、第二产业、第三产业增加值与增长率情况如图所示: 
根据图中信息,写成下列填空:
(1)第三产业的增加值为亿元:
(2)第三产业的增长率是第一产业增长率的倍(精确到0.1);
(3)三个产业中第产业的增长最快.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知P是线段AB的黄金分割点,且PA>PB,若S1表示PA为一边的正方形的面积,S2表示长是AB,宽是PB的矩形的面积,则S1S2 . (填“>”“=”或“<”) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以M(﹣5,0)为圆心、4为半径的圆与x轴交于A、B两点,P是⊙M上异于A、B的一动点,直线PA、PB分别交y轴于C、D,以CD为直径的⊙N与x轴交于E、F,则EF的长( ) 
A.等于4 ![]()
B.等于4 ![]()
C.等于6
D.随P点位置的变化而变化
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,二次函数y=﹣ ![]() x2+bx+c的图象经过B、C两点.
x2+bx+c的图象经过B、C两点.
(1)求该二次函数的解析式;
(2)结合函数的图象探索:当y>0时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,规定把一个三角形先沿着x轴翻折,再向右平移2个单位称为1次变换.如图,已知等边三角形ABC的顶点B、C的坐标分别是(﹣1,﹣1)、(﹣3,﹣1),把△ABC经过连续9次这样的变换得到△A′B′C′,则点A的对应点A′的坐标是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com