
【题目】如图,在平面直角坐标系中,以(1,0)为圆心的⊙P与y轴相切于原点O,过点A(-1,0)的直线AB与⊙P相切于点B.
(1)求AB的长.
(2)求AB、OA与![]() 所围成的阴影部分面积.
所围成的阴影部分面积.
(3)求直线AB的解析式.
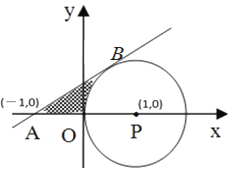
【答案】(1)![]() ;(2)
;(2)![]()
![]() ;(3)
;(3)![]() .
.
【解析】
1)连接PB,由于A、P的坐标已知,因此求出OA、AP的长度,根据直线AB与⊙P相切于点B,⊙P与y轴相切于原点O,利用勾股定理定理可以求出AB的长度;
(2)连接OB,利用(1)的结果可以得到∠OPB=60°,根据![]() 即可求出阴影部分面积;
即可求出阴影部分面积;
(3)设直线AB与y轴相交于点C,根据已知条件可以得到∠BAP=30°,而OA=1,因此可以求出CO的长度,即求出了C的坐标,而A的坐标已知,再利用待定系数法即可求出AB的解析式;
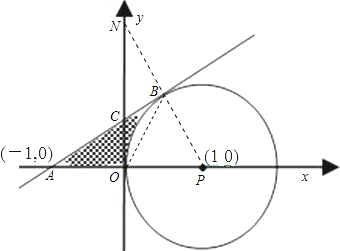
解:(1)连接PB
∵点A、P的坐标分别为(-1,0)、(1,0),
∴OA=OP=1,
∴PA=2.
∵直线AB与⊙P相切于点B,
∴PB⊥AB,
∴∠ABP=90°
又∵⊙P与y轴相切于原点O,
∴PB=OP=1,
∴![]() ;
;
(2)连接OB
∵∠ABP=90°,OA=OP,
∴![]() ,
,
又∵PB=OP,
∴PB=OP=OB,
∴∠OPB=60°,
∴![]()
![]() ;
;
(3)如图示,设直线AB与y轴相交于点C
∵∠OPB=60°,∠ABP=90°,
∴∠BAP=180°-60°-90°=30°,
∴在Rt△OAC中,![]() ,
,
设OC=x,则AC=2x,
依题意得(2x)2=x2+12,
解得![]()
∵x>0,
∴![]() ;
;
∴点C坐标为(0,![]() ),
),
可设直线AB的解析式为![]() (k≠0),
(k≠0),
∵直线AB过点A(-1,0),
∴![]() ,
,
∴![]() ,
,
∴直线AB的解析式为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,一条顶点坐标为![]() 的抛物线与y轴交于点C(0,5).与x轴交于点A和点B(点B在点A右侧),有一宽度为1.长崖足够的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和点Q(点P在点Q右侧),交直线AC于点M和点N(点M在点N右侧),交x轴于点E和点F(点E在点F右侧)
的抛物线与y轴交于点C(0,5).与x轴交于点A和点B(点B在点A右侧),有一宽度为1.长崖足够的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和点Q(点P在点Q右侧),交直线AC于点M和点N(点M在点N右侧),交x轴于点E和点F(点E在点F右侧)
(1)求抛物线的解析式;
(2)当点M和点N都在线段AC上时,连接MF,如果![]() ,求点Q的坐标;
,求点Q的坐标;
(3)在矩形平移的过程中,当以点P、Q、M、N为顶点的四边形是平行四边形时,直接写出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
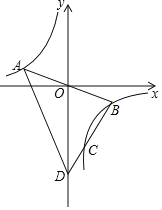
【题目】如图,反比例函数y=![]() (k≠0)的图象经过△ABD的顶点A,B,交BD于点C,AB经过原点,点D在y轴上,若BD=4CD,△OBD的面积为15,则k的值为_____.
(k≠0)的图象经过△ABD的顶点A,B,交BD于点C,AB经过原点,点D在y轴上,若BD=4CD,△OBD的面积为15,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
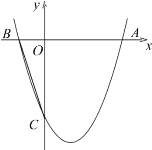
【题目】如图,二次函数![]() 的图像与x轴交于A,B两点(点B在点A左侧),与y轴负半轴相交于点C,且tan∠ABC=3,
的图像与x轴交于A,B两点(点B在点A左侧),与y轴负半轴相交于点C,且tan∠ABC=3,
(1)求该二次函数的解析式;
(2)设E是位于第四象限抛物线上的一个动点,过E作x轴的平行线交抛物线于另一点F,过点F作FG垂直于x轴于点G,再过点E作EH垂直于x轴于点H,得到矩形EFGH,则在点E运动过程中,当矩形EFGH为正方形时,求出该正方形的边长;
(3)设点P是x轴下方的抛物线上的一个动点,连接PA、PC,求△PAC面积的取值范围,当△PAC面积为整数时,这样的△PAC有几个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=﹣m与y轴交于点A,直线a:y=x+m与y轴交于点B,抛物线y=x2+mx的顶点为C,且与x轴左交点为D(其中m>0).
(1)当AB=12时,在抛物线的对称轴上求一点P使得△BOP的周长最小;
(2)当点C在直线l上方时,求点C到直线l距离的最大值;
(3)若把横坐标、纵坐标都是整数的点称为“整点”.当m=2020时,求出在抛物线和直线a所围成的封闭图形的边界上的“整点”的个数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市中招体育测试改革,其中篮球和足球作为选考项目,某商店抓住这一商机决定购进一批篮球和足球共200个,这两种球的进价和售价如下表所示:
篮球 | 足球 | |
进价(元/个) | 180 | 150 |
售价(元/个) | 250 | 200 |
(1)若商店计划销售完这批球后能获利11600元,问篮球和足球应分别购进多少个?
(2)设购进篮球![]() 个,获利为
个,获利为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系;
之间的函数关系;
(3)若商店计划投入资金不多于31560元且销售完这批球后商店获利不少于11000元,请问有哪几种购球方案,并写出获利最大的购球方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
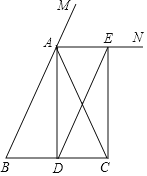
【题目】已知:如图,在△ABC中,AB=AC,AD是△ABC的中线,AN为△ABC的外角∠CAM的平分线,CE∥AD,交AN于点E.求证:四边形ADCE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】配餐公司为某学校提供A、B、C三类午餐供师生选择,三类午餐每份的价格分别是:A餐5元,B餐6元,C餐8元.为做好下阶段的营销工作,配餐公司根据该校上周A、B、C三类午餐购买情况,将所得的数据处理后,制成统计表(如下左图);根据以往销售量与平均每份利润之间的关系,制成统计图(如下右图).
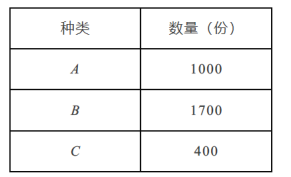
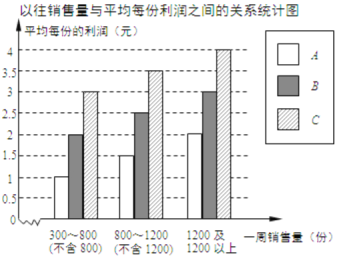
请根据以上信息,解答下列问题:
(1)该校师生上周购买午餐费用的众数是 元;
(2)配餐公司上周在该校销售B餐每份的利润大约是 元;
(3)请你计算配餐公司上周在该校销售午餐约盈利多少元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com