
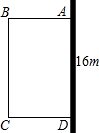
 用一段长为40米的篱笆围成一边靠墙的草坪,墙长16米,当这个矩形的一边BC为多少时,草坪面积最大?最大面积为多少.
用一段长为40米的篱笆围成一边靠墙的草坪,墙长16米,当这个矩形的一边BC为多少时,草坪面积最大?最大面积为多少. 分析 设养鸡场宽AB为x米,则长BC为40-2x米,由面积公式写出y与x的函数关系式,然后利用二次函数的最值的知识可得出菜园的最大面积,及取得最大面积时矩形的长BC.
解答 解:设矩形的宽AB为xm,长BC为40-2x米,面积为Sm2,根据题意得:
S=x(40-2x)
=-2x2+40x
=-2(x-10)2+200,
所以,当x=10时,S最大,最大值为200,但40-2x=20>16,不合题意,
因此当矩形的长BC为16m(不超过墙长),宽AB为12m时,矩形草坪的面积最大,最大面积为16×12=192m2.
点评 本题主要考查二次函数的应用,关键在于找出等量关系列出方程求解,另外应注意配方法求最大值在实际中的应用.


科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{5}$ | D. | 1+$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
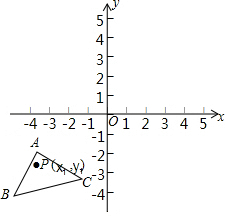 如图,已知A(-4,-1),B(-5,-4),C(-1,-3),△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).
如图,已知A(-4,-1),B(-5,-4),C(-1,-3),△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 点A在⊙O外 | B. | 点A在⊙O上 | C. | 点A在⊙O 内 | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com