
【题目】如图1.在△ABC中,矩形EFGH的一边EF在AB上,顶点G、H分别在BC、AC上,CD是边AB上的高,CD交GH于点I.若CI=4,HI=3,AD![]() .矩形DFGI恰好为正方形.
.矩形DFGI恰好为正方形.
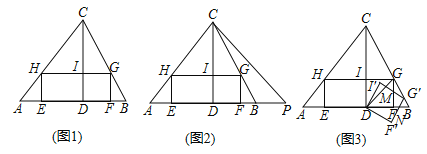
(1)求正方形DFGI的边长;
(2)如图2,延长AB至P.使得AC=CP,将矩形EFGH沿BP的方向向右平移,当点G刚好落在CP上时,试判断移动后的矩形与△CBP重叠部分的形状是三角形还是四边形,为什么?
(3)如图3,连接DG,将正方形DFGI绕点D顺时针旋转一定的角度得到正方形DF′G′I′,正方形DF′G′I′分别与线段DG、DB相交于点M、N,求△MNG′的周长.
【答案】(1)2;(2)三角形;(3)4.
【解析】
(1)由HI∥AD,得到![]() ,求出AD即可解决问题;
,求出AD即可解决问题;
(2)如图2中,设点G落在PC时对应的点为G′,点F的对应的点为F′.求出IG′和BD的长比较即可判定;
(3)如图3中,如图将△DMI′绕点D逆时针旋转90°得到△DF′R,此时N、F′、R共线.想办法证明MN=MI′+NF′,即可解决问题.
(1)∵HI∥AD,
∴![]() ,
,
∴![]() ,
,
∴AD=6,
∴ID=CD﹣CI=2,∴正方形的边长为2;
(2)三角形,理由如下:
如图2中,设点G落在PC时对应的点为G′,点F的对应的点为F′.
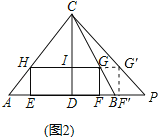
∵CA=CP,CD⊥PA,∴∠ACD=∠PCD,∠A=∠P,
∵HG′∥PA,
∴∠CHG′=∠A,∠CG′H=∠P,
∴∠CHG′=∠CG′H,∴CH=CG′,
∴IH=IG′=DF′=3,
∵IG∥DB,∴![]() ,
,
∴![]() ,∴DB=3,
,∴DB=3,
∴DB=DF′=3,∴点B与点F′重合,
∴移动后的矩形与△CBP重叠部分是△BGG′,
∴移动后的矩形与△CBP重叠部分的形状是三角形;
(3)如图3中,如图将△DMI′绕点D逆时针旋转90°得到△DF′R,此时N、F′、R共线.
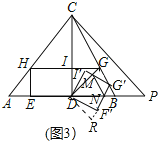
∵∠MDN=∠NDF+∠MDI′=∠NDF′+∠DF′R=∠NDR=45°,
∵DN=DN,DM=DR,
∴△NDM≌△NDR,
∴MN=NR=NF′+RF′=NF′+MI′,
∴△MNG′的周长=MN+MG′+NG′=MG′+MI′+NG′+F′R=2I′G′=4.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,将一块正方形纸板OEFG如图1摆放,它的顶点O与矩形ABCD的对角线交点重合,点A在正方形的边OG上,现将正方形绕点O逆时针旋转,当点B在OG边上时,停止旋转,在旋转过程中OG交AB于点M,OE交AD于点N.
(1)开始旋转前,即在图1中,连接NC.
①求证:NC=NA(M);
②若图1中NA(M)=4,DN=2,请求出线段CD的长度.
(2)在图2(点B在OG上)中,请问DN、AN、CD这三条线段之间有什么数量关系?写出结论,并说明理由.
(3)试探究图3中AN、DN、AM、BM这四条线段之间有什么数量关系?写出结论,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3700米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°,求这座山的高度CD.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设P(x,0)是x轴上的一个动点,它与原点的距离为y1.
(1)求y1关于x的函数解析式,并画出这个函数的图象;
(2)若反比例函数y2![]() 的图象与函数y1的图象相交于点A,且点A的纵坐标为2.
的图象与函数y1的图象相交于点A,且点A的纵坐标为2.
①求k的值;
②结合图象,当y1>y2时,写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】永州植物园“清风园”共设11个主题展区.为推进校园文化建设,某校九年级(1)班组织部分学生到“清风园”参观后,开展“我最喜欢的主题展区”投票调查.要求学生从“和文化”、“孝文化”、“德文化”、“理学文化”、“瑶文化”五个展区中选择一项,根据调查结果绘制出了两幅不完整的条形统计图和扇形统计图.结合图中信息,回答下列问题.
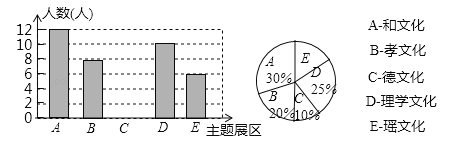
(1)参观的学生总人数为 人;
(2)在扇形统计图中最喜欢“瑶文化”的学生占参观总学生数的百分比为 ;
(3)补全条形统计图;
(4)从最喜欢“德文化”的学生中随机选两人参加知识抢答赛,最喜欢“德文化”的学生甲被选中的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】布袋里有四个小球,球表面分别标有2、3、4、6四个数字,它们的材质、形状、大小完全相同。从中随机摸出一个小球记下数字为x,再从剩下的三个球中随机摸出一个球记下数字为y,点A的坐标为(x,y).运用画树状图或列表的方法,写出A点所有可能的坐标,并求出点A在反比例函数![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求以C、E、F为顶点三角形与△COD相似时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我区电视台举行的“讲故事”比赛中,甲、乙、丙三位评委,对选手的综合表现,分别给出“待定”或“通过” 的结论.
(1)利用树状图写出三位评委给出选手A的所有可能的结论;
(2)对于选手A,只有甲、乙两位评委给出相同结论的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com