练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某校数学课外小组，在坐标纸上为某湿地公园的一块空地设计植树方案如下：第k棵树种植在点Pk（xk，yk）处，其中x1＝1，y1＝1，且k≥2时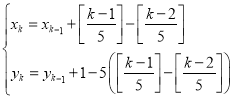，，[a]表示非负实数a的整数部分，例如[2.3]＝2，，[0.5]＝0．按此方案，第2019棵树种植点的坐标应为（　　）

    A.(6，2020)B.(2019，5)C.(3，403)D.(404，4)

    【答案】D

    【解析】

    根据已知分别求出1≤k≤5时，P点坐标为（1，1）、（1，2）、（1，3）、（1，4）、（1，5），当6≤k≤10时，P点坐标为（2，1）、（2，2）、（2，3）、（2，4）、（2，5），通过观察得到点的坐标特点，进而求解．

    解：由题可知1≤k≤5时，P点坐标为（1，1）、（1，2）、（1，3）、（1，4）、（1，5），

    当6≤k≤10时，P点坐标为（2，1）、（2，2）、（2，3）、（2，4）、（2，5），

    ……

    通过以上数据可得，P点的纵坐标5个一组循环，

    ∵2019÷5＝403…4，

    ∴当k＝2019时，P点的纵坐标是4，横坐标是403+1＝404，

    ∴P（404，4），

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下面是小东设计的“作圆的一个内接矩形，并使其对角线的夹角为60°”的尺规作图过程

    已知：⊙O

    求作：矩形ABCD，使得矩形ABCD内接于⊙O，且其对角线AC，BD的夹角为60°．

    作法：如图

    ①作⊙O的直径AC；

    ②以点A为圆心，AO长为半径画弧，交直线AC上方的圆弧于点B；

    ③连接BO并延长交⊙O于点D；

    所以四边形ABCD就是所求作的矩形.

    根据小东设计的尺规作图过程，

    (1)使用直尺和圆规，补全图形(保留作图痕迹)；

    (2)完成下面的证明．

    证明：∵点A，C都在⊙O上，

    ∴OA=OC

    同理OB=OD

    ∴四边形ABCD是平行四边形

    ∵AC是⊙O的直径，

    ∴∠ABC=90° （ ）（填推理的依据）

    ∴四边形ABCD是矩形

    ∵AB= =BO，

    ∴四边形ABCD四所求作的矩形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

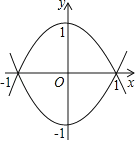
    【题目】如图，已知将抛物线y＝x2﹣1沿x轴向上翻折与所得抛物线围成一个封闭区域（包括边界），在这个区域内有5个整点（点M满足横、纵坐标都为整数，则把点M叫做“整点”），它们分别是（1，0），（﹣1，0），（0，0），（0，1），（0，﹣1）．现将抛物线y＝a（x+1）2+2（a＜0）沿x轴向下翻折，所得抛物线与原抛物线所围成的封闭区域内（包括边界）恰有11个整点，则a的取值范围是（　　）

    A.﹣1＜a＜﹣B.a＜﹣1C.a＜﹣D.﹣1≤a＜﹣

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AB是⊙O的直径，BC是⊙O的切线，连接AC与⊙O交于点 D．取BC的中点E，连接DE，并连接OE交⊙O于点F．连接AF交BC于点G，连接BD交AG于点H．

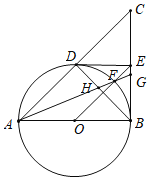
    （1）若EF＝1，BE＝，求∠EOB的度数；

    （2）求证：DE为⊙O的切线；

    （3）求证：点F为线段HG的中点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一块长30cm，宽12cm的矩形铁皮，

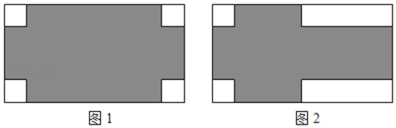
    （1）如图1，在铁皮的四角各切去一个同样的正方形，然后将四周突出部分折起，就能制作成一个底面积为144cm2的无盖方盒，如果设切去的正方形的边长为xcm，则可列方程为　 　．

    （2）由于实际需要，计划制作一个有盖的长方体盒子，为了合理使用材料，某学生设计了如图2的裁剪方案，空白部分为裁剪下来的边角料，其中左侧两个空白部分为正方形，问能否折出底面积为104cm2的有盖盒子（盒盖与盒底的大小形状完全相同）？如果能，请求出盒子的体积；如果不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

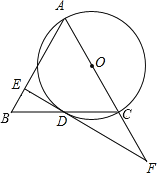
    【题目】如图，以等腰△ABC的一腰AC为直径作⊙O，交底边BC于点D，过点D作腰AB的垂线，垂足为E，交AC的延长线于点F．

    （1）求证：EF是⊙O的切线；

    （2）证明：∠CAD＝∠CDF；

    （3）若∠F＝30°，AD＝，求⊙O的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y＝ax2＋bx＋c上部分点的横坐标x，纵坐标y 的对应值如表所示:

    给出下列说法：①抛物线与y轴的交点为(0，6)； ②抛物线的对称轴是在y轴的右侧；③抛物线一定经过点(3，0)； ④在对称轴左侧，y随x增大而减小．从表中可知，下列说法正确的个数有( )

    A.1个B.2个C.3个D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

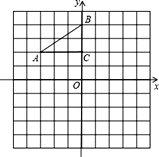
    【题目】如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（﹣3，2），B（0，4），C（0，2）．

    （1）将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A1B1C1，平移△ABC，若点A的对应点A2的坐标为（0，﹣4），画出平移后对应的△A2B2C2；

    （2）若将△A1B1C1绕某一点旋转可以得到△A2B2C2，请直接写出旋转中心的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ABC=90°，tan∠BAC=2，A（0，a），B（b，0），点C在第二象限，BC与y轴交于点D（0，c），若y轴平分∠BAC，则点C的坐标不能表示为（　　）

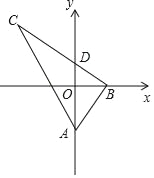
    A. （b+2a，2b） B. （﹣b﹣2c，2b）

    C. （﹣b﹣c，﹣2a﹣2c） D. （a﹣c，﹣2a﹣2c）

    查看答案和解析>>

    同步练习册答案