
ЁОЬтФПЁПвЛПщГЄ30cmЃЌПэ12cmЕФОиаЮЬњЦЄЃЌ
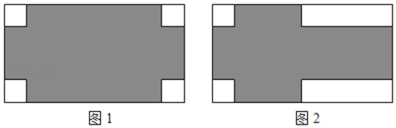
ЃЈ1ЃЉШчЭМ1ЃЌдкЬњЦЄЕФЫФНЧИїЧаШЅвЛИіЭЌбљЕФе§ЗНаЮЃЌШЛКѓНЋЫФжмЭЛГіВПЗжелЦ№ЃЌОЭФмжЦзїГЩвЛИіЕзУцЛ§ЮЊ144cm2ЕФЮоИЧЗНКаЃЌШчЙћЩшЧаШЅЕФе§ЗНаЮЕФБпГЄЮЊxcmЃЌдђПЩСаЗНГЬЮЊЁЁ ЁЁЃЎ
ЃЈ2ЃЉгЩгкЪЕМЪашвЊЃЌМЦЛЎжЦзївЛИігаИЧЕФГЄЗНЬхКазгЃЌЮЊСЫКЯРэЪЙгУВФСЯЃЌФГбЇЩњЩшМЦСЫШчЭМ2ЕФВУМєЗНАИЃЌПеАзВПЗжЮЊВУМєЯТРДЕФБпНЧСЯЃЌЦфжазѓВрСНИіПеАзВПЗжЮЊе§ЗНаЮЃЌЮЪФмЗёелГіЕзУцЛ§ЮЊ104cm2ЕФгаИЧКазгЃЈКаИЧгыКаЕзЕФДѓаЁаЮзДЭъШЋЯрЭЌЃЉЃПШчЙћФмЃЌЧыЧѓГіКазгЕФЬхЛ§ЃЛШчЙћВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉЃЈ30Љ2xЃЉЃЈ12Љ2xЃЉЃН144ЃЛЃЈ2ЃЉФмелГіЕзУцЛ§ЮЊ104cm2ЕФгаИЧКазгЃЌКазгЕФЬхЛ§ЮЊ208m3
ЁОНтЮіЁП
ЃЈ1ЃЉЩшЧаШЅЕФе§ЗНаЮЕФБпГЄЮЊxcmЃЌдђелГЩЕФЗНКаЕФЕзУцЮЊГЄЃЈ30Љ2xЃЉcmЃЌПэЮЊЃЈ12Љ2xЃЉcmЕФОиаЮЃЌИљОнОиаЮЕФУцЛ§ЙЋЪНЃЌМДПЩЕУГіЙигкxЕФвЛдЊЖўДЮЗНГЬЃЌДЫЮЪЕУНтЃЛ
ЃЈ2ЃЉЩшЧаШЅЕФе§ЗНаЮЕФБпГЄЮЊycmЃЌдђелГЩЕФГЄЗНЬхКазгЕФЕзУцЮЊГЄЃЈ![]() ЉyЃЉcmЃЌПэЮЊЃЈ12Љ2yЃЉcmЕФОиаЮЃЌИљОнОиаЮЕФУцЛ§ЙЋЪНЃЌМДПЩЕУГіЙигкyЕФвЛдЊЖўДЮЗНГЬЃЌНтжЎШЁЦфНЯаЁжЕЃЌдйРћгУГЄЗНЬхЕФЬхЛ§ЙЋЪНМДПЩЧѓГіНсТлЃЎ
ЉyЃЉcmЃЌПэЮЊЃЈ12Љ2yЃЉcmЕФОиаЮЃЌИљОнОиаЮЕФУцЛ§ЙЋЪНЃЌМДПЩЕУГіЙигкyЕФвЛдЊЖўДЮЗНГЬЃЌНтжЎШЁЦфНЯаЁжЕЃЌдйРћгУГЄЗНЬхЕФЬхЛ§ЙЋЪНМДПЩЧѓГіНсТлЃЎ
НтЃКЃЈ1ЃЉЩшЧаШЅЕФе§ЗНаЮЕФБпГЄЮЊxcmЃЌдђелГЩЕФЗНКаЕФЕзУцЮЊГЄЃЈ30Љ2xЃЉcmЃЌПэЮЊЃЈ12Љ2xЃЉcmЕФОиаЮЃЌ
вРЬтвтЃЌЕУЃКЃЈ30Љ2xЃЉЃЈ12Љ2xЃЉЃН144ЃЎ
ЙЪД№АИЮЊЃКЃЈ30Љ2xЃЉЃЈ12Љ2xЃЉЃН144ЃЎ
ЃЈ2ЃЉЩшЧаШЅЕФе§ЗНаЮЕФБпГЄЮЊycmЃЌдђелГЩЕФГЄЗНЬхКазгЕФЕзУцЮЊГЄЃЈ![]() ЉyЃЉcmЃЌПэЮЊЃЈ12Љ2yЃЉcmЕФОиаЮЃЌ
ЉyЃЉcmЃЌПэЮЊЃЈ12Љ2yЃЉcmЕФОиаЮЃЌ
вРЬтвтЃЌЕУЃКЃЈ![]() ЉyЃЉЃЈ12Љ2yЃЉЃН104ЃЌ
ЉyЃЉЃЈ12Љ2yЃЉЃН104ЃЌ
ећРэЃЌЕУЃКy2Љ21y+38ЃН0ЃЌ
НтЕУЃКy1ЃН2ЃЌy2ЃН19ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЌ
ЁрКазгЕФЬхЛ§ЃН104ЁС2ЃН208ЃЈcm3ЃЉЃЎ
Д№ЃКФмелГіЕзУцЛ§ЮЊ104cm2ЕФгаИЧКазгЃЌКазгЕФЬхЛ§ЮЊ208m3ЃЎ


 ЬвРюЮФЛЏПьРжЪюМйЮфККГіАцЩчЯЕСаД№АИ
ЬвРюЮФЛЏПьРжЪюМйЮфККГіАцЩчЯЕСаД№АИ гХауЩњПьРжМйЦкУПвЛЬьШЋаТКЎМйзївЕБОЯЕСаД№АИ
гХауЩњПьРжМйЦкУПвЛЬьШЋаТКЎМйзївЕБОЯЕСаД№АИ ЪюМйНгСІШќаТНЎЧрЩйФъГіАцЩчЯЕСаД№АИ
ЪюМйНгСІШќаТНЎЧрЩйФъГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
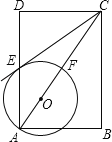
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌЕуOдкЖдНЧЯпACЩЯЃЌвдOAЕФГЄЮЊАыОЖЕФЁбOгыADЁЂACЗжБ№НЛгкЕуEЁЂFЃЌЧвЁЯACBЃНЁЯDCEЃЎ
ЃЈ1ЃЉХаЖЯжБЯпCEгыЁбOЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєABЃН![]() ЃЌBCЃН2ЃЌЧѓЁбOЕФАыОЖЃЎ
ЃЌBCЃН2ЃЌЧѓЁбOЕФАыОЖЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкБпГЄЮЊ1ЕФаЁе§ЗНаЮзщГЩЕФЭјИёжаЃЌЁїAOBЕФШ§ИіЖЅЕуОљдкИёЕуЩЯЃЌЕуAЁЂBЕФзјБъЗжБ№ЮЊЃЈ3ЃЌ2ЃЉЁЂЃЈ1ЃЌ3ЃЉЃЎЁїAOBШЦЕуOФцЪБеыа§зЊ90КѓЕУЕНЁїA1OB1ЃЎ
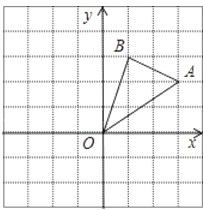
ЃЈ1ЃЉдкЭјИёжаЛГіЁїA1OB1ЃЌВЂБъЩЯзжФИЃЛ
ЃЈ2ЃЉЕуAЙигкOЕужааФЖдГЦЕФЕуЕФзјБъЮЊ ЃЛ
ЃЈ3ЃЉЕуA1ЕФзјБъЮЊ ЃЛ
ЃЈ4ЃЉдка§зЊЙ§ГЬжаЃЌЕуBОЙ§ЕФТЗОЖЮЊЛЁBB1ЃЌФЧУДЛЁBB1ЕФГЄЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЪЧ
ЪЧ![]() ЕФжБОЖЃЌ
ЕФжБОЖЃЌ![]() ЁЂ
ЁЂ![]() ЮЊ
ЮЊ![]() ЩЯЕФЕуЃЌШє
ЩЯЕФЕуЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌШє
ЃЌШє![]() ЦНЗж
ЦНЗж![]() ЃЌдђ
ЃЌдђ![]() ГЄЮЊЃЈ ЃЉ
ГЄЮЊЃЈ ЃЉ
A.10B.7C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈЮЊЗНБуД№ЬтЃЌПЩдкД№ЬтПЈЩЯЛГіФуШЯЮЊБивЊЕФЭМаЮЃЉ
дкRtЁїABCжаЃЌЁЯA=90ЁуЃЌAC=AB=4ЃЌDЃЌEЗжБ№ЪЧБпABЃЌACЕФжаЕуЃЎШєЕШбќRtЁїADEШЦЕуAФцЪБеыа§зЊЃЌЕУЕНЕШбќRtRtЁїAD1E1ЃЌЩша§зЊНЧЮЊІСЃЈ0ЃМІСЁм180ЁуЃЉЃЌМЧжБЯпBD1гыCE1ЕФНЛЕуЮЊPЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕБІС=90ЁуЪБЃЌЯпЖЮBD1ЕФГЄЕШгк ЃЌЯпЖЮCE1ЕФГЄЕШгк ЃЛЃЈжБНгЬюаДНсЙћЃЉ
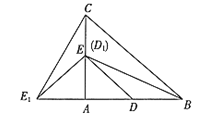
ЃЈ2ЃЉШчЭМ2ЃЌЕБІС=135ЁуЪБЃЌЧѓжЄЃКBD1=CE1 ЃЌЧвBD1ЁЭCE1 ЃЛ
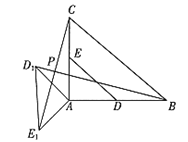
ЃЈ3ЃЉЧѓЕуPЕНABЫљдкжБЯпЕФОрРыЕФзюДѓжЕЃЎЃЈжБНгаДГіНсЙћЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЪ§бЇПЮЭтаЁзщЃЌдкзјБъжНЩЯЮЊФГЪЊЕиЙЋдАЕФвЛПщПеЕиЩшМЦжВЪїЗНАИШчЯТЃКЕкkПУЪїжжжВдкЕуPkЃЈxkЃЌykЃЉДІЃЌЦфжаx1ЃН1ЃЌy1ЃН1ЃЌЧвkЁн2ЪБЃЌ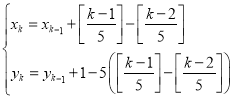 ЃЌ[a]БэЪОЗЧИКЪЕЪ§aЕФећЪ§ВПЗжЃЌР§Шч[2.3]ЃН2ЃЌ
ЃЌ[a]БэЪОЗЧИКЪЕЪ§aЕФећЪ§ВПЗжЃЌР§Шч[2.3]ЃН2ЃЌ![]() ЃЌ[0.5]ЃН0ЃЎАДДЫЗНАИЃЌЕк2019ПУЪїжжжВЕуЕФзјБъгІЮЊЃЈЁЁЁЁЃЉ
ЃЌ[0.5]ЃН0ЃЎАДДЫЗНАИЃЌЕк2019ПУЪїжжжВЕуЕФзјБъгІЮЊЃЈЁЁЁЁЃЉ
A.(6ЃЌ2020)B.(2019ЃЌ5)C.(3ЃЌ403)D.(404ЃЌ4)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
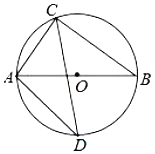
ЁОЬтФПЁПШчЭМЃЌдкБпГЄЮЊ1ЕФаЁе§ЗНаЮЭјИёжаЃЌЕуAЁЂBЁЂCЁЂDЖМдкетаЉаЁе§ЗНаЮЕФЖЅЕуЩЯЃЌABЁЂCDЯрНЛгкЕуOЃЌдђtanЁЯAOD=________.
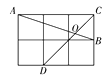
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§y=k1x+b(k1Ёй0)гыЗДБШР§КЏЪ§![]() ЕФЭМЯѓНЛгкЕуA(-1ЃЌ2)ЃЌB(mЃЌ-1)ЃЎ
ЕФЭМЯѓНЛгкЕуA(-1ЃЌ2)ЃЌB(mЃЌ-1)ЃЎ
(1)ЧѓвЛДЮКЏЪ§гыЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
(2)дкxжсЩЯЪЧЗёДцдкЕуP(nЃЌ0)ЃЌЪЙЁїABPЮЊЕШбќШ§НЧаЮЃЌЧыФужБНгаДГіPЕуЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНќФъРДЃЌЁАдкГѕжаЪ§бЇНЬбЇКђзмЪЙгУМЦЫуЦїЪЧЗёжБНггАЯьбЇЩњМЦЫуФмСІЕФЗЂеЙЁБетвЛЮЪЬтЪмЕНСЫЙуЗКЙизЂЃЌЮЊДЫЃЌФГаЃЫцЛњЕїВщСЫnУћбЇЩњЖдДЫЮЪЬтЕФПДЗЈЃЈПДЗЈЗжЮЊШ§жжЃКУЛгагАЯьЃЌгАЯьВЛДѓЃЌгАЯьКмДѓЃЉЃЌВЂНЋЕїВщНсЙћ ЛцжЦГЩШчЯТВЛЭъећЕФЭГМЦБэКЭЩШаЮЭГМЦЭМЃЌИљОнЭГМЦЭМБэЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
nУћбЇЩњЖдЪЙгУМЦЫуЦїгАЯьМЦЫуФмСІЕФЗЂеЙПДЗЈШЫЪ§ЭГМЦБэ
ПДЗЈ | УЛгагАЯь | гАЯьВЛДѓ | гАЯьКмДѓ |
бЇЩњШЫЪ§ЃЈШЫЃЉ | 40 | 60 | m |

ЃЈ1ЃЉЧѓnЕФжЕЃЛ
ЃЈ2ЃЉЭГМЦБэжаЕФm= ЃЛ
ЃЈ3ЃЉЙРМЦИУаЃ1800УћбЇЩњжаШЯЮЊЁАгАЯьКмДѓЁБЕФбЇЩњШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com