练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，点B，C，E，F在一直线上，AB∥DC，DE∥GF，∠B=∠F=72°，则∠D=度．

    【答案】36
    【解析】解：∵AB∥DC，DE∥GF，∠B=∠F=72°， ∴∠DCE=∠B=72°，∠DEC=∠F=72°，
    在△CDE中，∠D=180°﹣∠DCE﹣∠DEC=180°﹣72°﹣72°=36°．
    所以答案是：36．
    【考点精析】通过灵活运用平行线的性质和三角形的内角和外角，掌握两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知边长为a的正方形的面积为8，则下列说法中，错误的是（ ）
    A.a是无理数
    B.a是方程x2﹣8=0的一个解
    C.a是8的算术平方根
    D.a满足不等式组

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1所示，从边长为a的正方形纸片中剪去一个边长为b的小正方形，再沿着线段AB剪开，把剪成的两张纸拼成如图2的等腰梯形，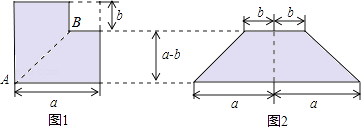
    （1）设图1中阴影部分面积为S1 ， 图2中阴影部分面积为S2 ， 请直接用含a、b的代数式表示S1和S2；
    （2）请写出上述过程所揭示的乘法公式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个不透明的袋中装有5个黄球，13个黑球和22个红球，它们除颜色外都相同．
    （1）求从袋中摸出一个球是黄球的概率；
    （2）现从袋中取出若干个黑球，并放入相同数量的黄球，搅拌均匀后使从袋中摸出一个是黄球的概率不小于 ，问至少取出了多少个黑球？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校为美化校园，计划对面积为1800m2的区域进行绿化，安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍，并且在独立完成面积为400 m2区域的绿化时，甲队比乙队少用4天.

    （1）求甲、乙两工程队每天能完成绿化的面积分别是多少m2？

    （2）若学校每天需付给甲队的绿化费用是0.4万元，乙队为0.25万元，要使这次的绿化总费用不超过8万元，至少应安排甲队工作多少天？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点A在反比例函数y=﹣ （x＜0）的图象上移动，连接OA，作OB⊥OA，并满足∠OAB=30°．在点A的移动过程中，追踪点B形成的图象所对应的函数表达式为（ ）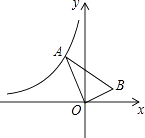
    A.y= （x＞0）
    B.y= （x＞0）
    C.y= （x＞0）
    D.y= （x＞0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用n边形的对角线把n边形分割成（n－2）个三角形，共有多少种不同的分割方案（n≥4）？

    （探究）为了解决上面的数学问题，我们采取一般问题特殊化的策略，先从最简单情形入手，再逐次递进转化，最后猜想得出结论．不妨假设n边形的分割方案有Pn种．

    探究一：用四边形的对角线把四边形分割成2个三角形，共有多少种不同的分割方案？

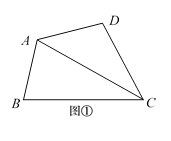
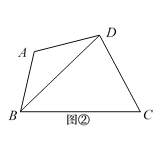
    如图①，图②，显然，只有2种不同的分割方案．所以，P4=2．

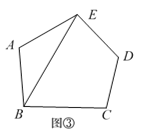
    探究二：用五边形的对角线把五边形分割成3个三角形，共有多少种不同的分割方案？

    不妨把分割方案分成三类：

    第1类：如图③，用A，E与B连接，先把五边形分割转化成1个三角形和1个四边形，再把四边形分割成2个三角形，由探究一知，有P4种不同的分割方案，所以，此类共有P4种不同的分割方案．

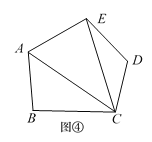
    第2类：如图④，用A，E与C连接，把五边形分割成3个三角形，有1种不同的分割方案，可视为种分割方案．

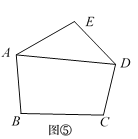
    第3类：图⑤，用A，E与D连接，先把五边形分割转化成1个三角形和1个四边形，再把四边形分割成2个三角形，由探究一知，有P4种不同的分割方案，所以，此类共有P4种不同的分割方案．

    所以，P5 =++=(种)

    探究三：用六边形的对角线把六边形分割成4个三角形，共有多少种不同的分割方案？

    不妨把分割方案分成四类：

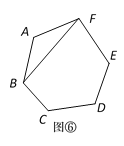
    第1类：如图⑥，用A，F与B连接，先把六边形分割转化成1个三角形和1个五边形，再把五边形分割成3个三角形，由探究二知，有P5种不同的分割方案．所以，此类共有P5种不同的分割方案．

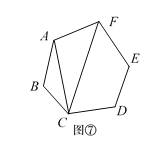
    第2类：如图⑦，用A，F与C连接，先把六边形分割转化成2个三角形和1个四边形．再把四边形分割成2个三角形，由探究一知，有P4种不同的分割方案．所以，此类共有P4种分割方案

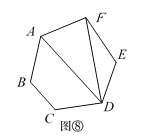
    第3类：如图⑧，用A，F与D连接，先把六边形分割转化成2个三角形和1个四边形．再把四边形分割成2个三角形，由探究一知，有P4种不同的分割方案．所以，此类共有P4种分割方案．

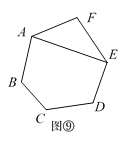
    第4类：如图⑨，用A，F与E连接，先把六边形分割转化成1个三角形和1个五边形．再把五边形分割成3个三角形，由探究二知，有P5种不同的分割方案．所以，此类共有P5种分割方案．

    所以，P6 =(种)

    探究四：用七边形的对角线把七边形分割成5个三角形，则P7与P6的关系为：

    P7 = ，共有_____种不同的分割方案．……

    （结论）用n边形的对角线把n边形分割成（n－2）个三角形，共有多少种不同的分割方案（n≥4）？（直接写出Pn与Pn -1的关系式，不写解答过程）．

    （应用）用八边形的对角线把八边形分割成6个三角形，共有多少种不同的分割方案？ （应用上述结论，写出解答过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图在△ABC中，DE∥BC，DF∥AC，则下列比例式不正确的是（ ）
    A. =
    B. =
    C. =
    D. =

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，抛物线y=ax2﹣5ax+4a与x轴交于A、B（A点在B点的左侧）与y轴交于点C．

    （1）如图1，连接AC、BC，若△ABC的面积为3时，求抛物线的解析式；
    （2）如图2，点P为第四象限抛物线上一点，连接PC，若∠BCP=2∠ABC时，求点P的横坐标；
    （3）如图3，在（2）的条件下，点F在AP上，过点P作PH⊥x轴于H点，点K在PH的延长线上，AK=KF，∠KAH=∠FKH，PF=﹣4 a，连接KB并延长交抛物线于点Q，求PQ的长．

    查看答案和解析>>

    同步练习册答案