
 在△ABC中,AB=AC,D是BC的中点,以AC为腰向外作等腰直角△ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.
在△ABC中,AB=AC,D是BC的中点,以AC为腰向外作等腰直角△ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.分析 (1)根据等腰直角三角形的旋转得出∠ABE=∠AEB,求出∠BAE,根据三角形内角和定理求出即可;
(2)根据等腰三角形的性质得出∠BAF=∠CAF,根据SAS推出△BAF≌△CAF,根据全等得出∠ABF=∠ACF,即可得出答案;
(3)根据全等得出BF=CF,求出∠CFG=∠EAG=90°,根据勾股定理求出EF2+BF2=EF2+CF2=EC2,EC2=AC2+AE2=2AC2,即可得出答案.
解答 (1)解:∵AB=AC,△ACE是等腰直角三角形,
∴AB=AE,
∴∠ABE=∠AEB,
又∵∠BAC=50°,∠EAC=90°,
∴∠BAE=50°+90°=140°,
∴∠AEB=(180°-140°)÷2=20°;
(2)证明:∵AB=AC,D是BC的中点,
∴∠BAF=∠CAF.
在△BAF和△CAF中,$\left\{\begin{array}{l}AB=AC\\∠BAF=∠CAF,AF=AF\end{array}$,
∴△BAF≌△CAF(SAS).
∴∠ABF=∠ACF.
又∵AB=AC,
∴∠ABE=∠AEB,
∴∠AEB=∠ACF.
(3)解:
∵△BAF≌△CAF,
∴BF=CF.
∴∠AEB=∠ACF,∠AGE=∠FGC.
∴∠CFG=∠EAG=90°.
∴EF2+BF2=EF2+CF2=EC2.
∵△ACE是等腰直角三角形,
∴∠CAE=90°,AC=AE.
∴EC2=AC2+AE2=2AC2=18.
即EF2+BF2=18.
故答案为:18.
点评 本题考查了勾股定理,全等三角形的性质和判定,等腰直角三角形的应用,能综合运用性质进行推理是解此题的关键,题目比较好,有一定的难度.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
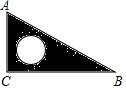 如图,一个直角三角形ABC的直角边BC=a,AC=b,三角形内部圆的半径为r.
如图,一个直角三角形ABC的直角边BC=a,AC=b,三角形内部圆的半径为r.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
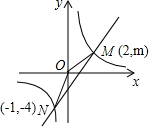 如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于M、N两点.
如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于M、N两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com