
分析 设每张车票的原价为a元,分别表示出第一种方案及第二种方案需要的付款,然后比较即可.
解答 解:设每张车票的原价为a元,按第一种方案购票应付款y1元,按第二种方案购票应付款y2元,
依题意得:y1=5a+a×60%•x,y2=(x+5)•a•70%,
①当y2>y1时,(x+5)•a•70%>5a+a×60%•x,
解得x>15,
②当y2=y1时,(x+5)•a•70%=5a+a×60%•x,
解得:x=15,
③当y2<y1时,(x+5)•a•70%<5a+a×60%x,
解得:x<15.
答:当学生多于15人时,按第一种方案;当学生等于15人时,两种方案都可以;当学生少于15人时,按第二种方案.
点评 本题考查的是一元一次不等式的应用,此类题目贴近生活,有利于培养学生应用数学解决生活中实际问题的能力,解题关键是要读懂题目的意思.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:选择题
| A. | y=-3(x+1)2-3 | B. | y=-3(x-1)2-3 | C. | y=-3(x+1)2+3 | D. | y=-3(x-1)2+3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
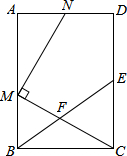 如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连结CF并延长交AB于点M,MN⊥CM交射线AD于点N.
如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连结CF并延长交AB于点M,MN⊥CM交射线AD于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在△ABC中,AB=AC,D是BC的中点,以AC为腰向外作等腰直角△ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.
在△ABC中,AB=AC,D是BC的中点,以AC为腰向外作等腰直角△ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
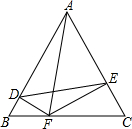 如图,△ABC是边长为8的等边三角形,F是边BC上的动点,且DF⊥AB,EF⊥AC.则四边形ADFE的面积最大值是12$\sqrt{3}$.
如图,△ABC是边长为8的等边三角形,F是边BC上的动点,且DF⊥AB,EF⊥AC.则四边形ADFE的面积最大值是12$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com