
【题目】以矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1),一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点A重合,此时抛物线的函数表达式为y=x2 , 再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
A.![]()
B.![]()
C.![]()
D.![]()
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:
【题目】如图1,![]() 和
和![]() 都是边长为1的等边三角形.
都是边长为1的等边三角形.
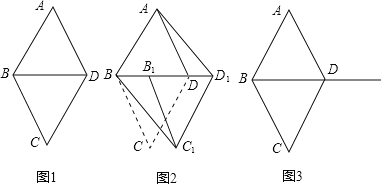
![]() 四边形ABCD是菱形吗?为什么?
四边形ABCD是菱形吗?为什么?
![]() 如图2,将
如图2,将![]() 沿射线BD方向平移到
沿射线BD方向平移到![]() 的位置,则四边形
的位置,则四边形![]() 是平行四边形吗?为什么?
是平行四边形吗?为什么?
![]() 在
在![]() 移动过程中,四边形
移动过程中,四边形![]() 有可能是矩形吗?如果是,请求出点B移动的距离
有可能是矩形吗?如果是,请求出点B移动的距离![]() 写出过程
写出过程![]() ;如果不是,请说明理由
;如果不是,请说明理由![]() 图3供操作时使用
图3供操作时使用![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,长方形ABCD中,AB=8,BC=10,在边CD上取一点E,将△ADE折叠后点D恰好落在BC边上的点F.
(1)求CE的长;
(2)建立平面直角坐标系如图②所示,在x轴上找一点P,使PA+PE的值最小,求出最小值和点P的坐标;
(3)如图③,DE的延长线与AF的延长线交于点G,在y轴上是否存在点M,使△FGM是直角三角形?如果存在,求出点M的坐标:如果不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京奥运会期间,某旅行社组团去北京观看某场足球比赛,入住某宾馆.已知该宾馆一楼房间比二楼房间少5间,该旅游团有48人,若全部安排在一楼,每间住4人,房间不够,每间住5人,有房间没住满.若全部安排在二楼,每间住3人,房间不够,每间住4人,则有房间没住满.你能根据以上信息确定宾馆一楼有多少房间吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.哥哥的身高比弟弟高是必然事件
B.今年的12月1日有雨是不确定事件
C.随机掷一枚均匀的硬币两次,都是正面朝上是不可能事件
D.“彩票中奖的概率为 ![]() ”表示买5张彩票肯定会中奖
”表示买5张彩票肯定会中奖
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果商贩老徐上水果批发市场进货,他了解到草莓的批发价格是每箱60元,苹果的批发价格是每箱40元.老徐购得草莓和苹果共60箱,刚好花费3100元.
(1)问草莓、苹果各购买了多少箱?
(2)老徐有甲、乙两家店铺,每售出一箱草莓或苹果,甲店分别获利15元和20元,乙店分别获利12元和16元.设老徐将购进的60箱水果分配给甲店草莓![]() 箱,苹果
箱,苹果![]() 箱,其余均分配给乙店.由于他口碑良好,两家店都很快卖完了这批水果.
箱,其余均分配给乙店.由于他口碑良好,两家店都很快卖完了这批水果.
①若老徐在甲店获利600元,则他在乙店获利多少元?
②若老徐希望获得总利润为1000元,则![]() =_______.(直接写出答案)
=_______.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:为缓解交通拥堵问题,小李将上班方式由自驾车改为骑电动车.他从家到达上班地点,自驾车要走的路程为10千米,骑电动车要走的路程为8千米,已知小李自驾车的速度是骑电动车速度的1.5倍,他由自驾车改为骑电动车后,时间多用了6分钟.求小李自驾车和骑电动车的速度分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的是用棋子成的T字形图案:
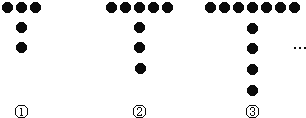
(1)填写下表:
图案序号 | ① | ② | ③ | ④ | …… | ⑧ |
每个图案中棋子的个数 | 5 | 8 | …… |
(2)第![]() 个“T“字形图案中棋子的个数为多少 (用含
个“T“字形图案中棋子的个数为多少 (用含![]() 的代数式表示);
的代数式表示);
(3)第20个“T”字形图案共有棋子多少个?
(4)计算前20个“T”字形图案中棋子的总个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com