
����Ŀ��������ƽ��ֱ������ϵ����ͼ1����ƽ���ڣ����ԭ���غϵ����������ֱ����ô���dz�����������ϵΪб����ϵ����P��б����ϵxOy�е�����һ�㣬����P�ֱ������������ƽ���ߣ���x�ᡢy�ύ�ڵ�M��N�����M��N��x�ᡢy���Ϸֱ��Ӧ��ʵ����a��b����ʱ��P������Ϊ��a��b����
��1����ͼ2����б����ϵxOy�У�������A����2��3����
��2����ͼ3����б����ϵxOy�У���֪��B��5��0����C��0��4������P��x��y�����߶�CB�ϵ�����һ�㣬��y��x֮��ĵ�����ϵʽΪ ��
��3������2���еĵ�P���߶�CB���ӳ����ϣ��������������䣬���жϣ�2���еĽ����Ƿ���Ȼ��������˵�����ɣ�
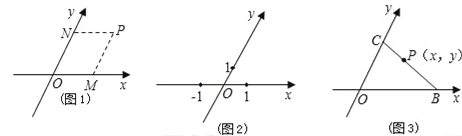
���𰸡���1������������2��3x+4y=12����3����Ȼ����
��������
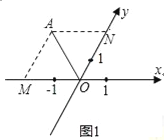
�����������1����AM��y�ᣬAM��x�ύ�ڵ�M��AN��x�ᣬAN��y�ύ�ڵ�N����������AMON��Ȼ��������ε������Լ��ȱ������ε��ж�����������OA�ij��ȣ�
��2������P�ֱ������������ƽ���ߣ���x�ᡢy�ύ�ڵ�M��N���� PN=x��PM=y������ƽ���߽��߶γɱ����ֱ��г�����x��y�ı���ʽ![]() ��
��![]() �������߶μ�ĺͲ��ϵ���PC+BP=BC֪
�������߶μ�ĺͲ��ϵ���PC+BP=BC֪![]() ��
��
��3������P���߶�BC���ӳ�����ʱ������������Ȼ�������������£���ʱ PN=��x��PM=y��֤������ͬ��2����
��1����AM��y�ᣬAM��x�ύ�ڵ�M��AN��x�ᣬAN��y�ύ�ڵ�N����������AMON��Ȼ��������ε������Լ��ȱ������ε��ж�����������OA�ij��ȣ�
��2������P�ֱ������������ƽ���ߣ���x�ᡢy�ύ�ڵ�M��N���� PN=x��PM=y������ƽ���߽��߶γɱ����ֱ��г�����x��y�ı���ʽ![]() ��
��![]() �������߶μ�ĺͲ��ϵ���PC+BP=BC֪
�������߶μ�ĺͲ��ϵ���PC+BP=BC֪![]() ��
��
��3������P���߶�BC���ӳ�����ʱ������������Ȼ�������������£���ʱ PN=��x��PM=y��֤������ͬ��2����
�����������1����ͼ1��AM��y�ᣬAM��x�ύ�ڵ�M��AN��x�ᣬAN��y�ύ�ڵ�N��
���ı���AMONΪƽ���ı��Σ���OM=ON��
��AMON������OM=AM
��OAƽ�֡�MON��
�֡ߡ�xOy=60�㣬
���MOA=60�㣬
���MOA�ǵȱ������Σ�
��OA=OM=2��
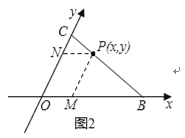
��2������P�ֱ������������ƽ���ߣ���x�ᡢy�ύ�ڵ�M��N��
�� PN=x��PM=y��
��PN��OB����![]() ��
��![]() ��
��
��PM��OC����![]() ����
����![]() ��
��
��![]() ��
��
�� 3x+4y=12��
�ʴ�Ϊ��3x+4y=12��
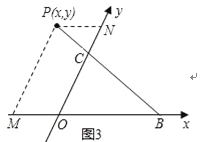
��3����2���еĽ�����Ȼ��������ͼ3������P���߶�BC���ӳ�����ʱ������������Ȼ�������������£���ʱ PN=��x��PM=y��
�루2�����ƣ�![]() ��
��![]() ��
��
�֡�![]() ��
��
��![]() ��
��![]() ��
��


 ��У��������ĩ��̾�ϵ�д�
��У��������ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A. ����һöӲ��10�Σ����泯�ϱ���5�Σ�
B. ��һ�����ӣ�����һ��������6��
C. Ϊ�˽�ij�ֵƹ��ʹ���������˲����ղ�ķ�����
D. ������Ľ�ˮ����Ϊ90%������ʾ�������90%�ĵط�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��AB�ǡ�O��ֱ������P���߶�AB���ӳ����ϣ�BP=OB=2����Q�ڡ�O�ϣ�����PQ��
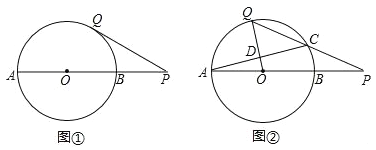
��1����ͼ�٣��߶�PQ���ڵ�ֱ�����O���У����߶�PQ�ij���
��2����ͼ�ڣ��߶�PQ���O����һ��������C����PC=CQ������OQ��AC���ڵ�D��
���ж�OQ��AC��λ�ù�ϵ����˵�����ɣ�
�����߶�PQ�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A. ����������DZ�Ȼ�¼�
B. �������¼������ĸ�����0
C. ��ˮƽ����������������һöͼ����һ���������
D. Ͷ��һö֮�ؽ��µ�Ӳ��1000�Σ����泯�µĴ���һ����500��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a����С����������b��a���෴����c�ľ���ֵΪ3����a��b��c��ֵΪ(����)
A. 3 B. ��3 C. 3��3 D. 0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ��ֱ����Բ�й����㣬��ô��ֱ����Բ��λ�ù�ϵ�ǣ�������
A. �ཻ B. ���� C. ���� D. �ཻ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ������ƽ������������������ͬ����ô������ǣ� ��
A����1 B��0 C��1 D��0��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ���У�������Գ��������ĶԳ�ͼ�ε��ǣ� ��
A. ����B. �ȱ�������C. ƽ���ı���D. ֱ��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com