Question

11．已知△ABC，AB=AC=5，BC=8，∠PDQ的顶点D在BC边上，DP交AB边于点E，DQ交AB边于点O且交CA的延长线于点F（点F与点A不重合），设∠PDQ=∠B，BD=3．
（1）求证：△BDE∽△CFD；
（2）设BE=x，OA=y，求y关于x的函数关系式，并写出定义域；
（3）当△AOF是等腰三角形时，求BE的长．

Answer 1

分析 （1）根据两角对应相等两三角形相似即可证明．
（2）过点D作DM∥AB交AC于M（如图1中）．由△BDE∽△CFD，得$\frac{CD}{BE}$=$\frac{FC}{BD}$，推出FC=$\frac{15}{x}$，由DM∥AB，得$\frac{DM}{AB}$=$\frac{CD}{CB}$，推出DM=$\frac{25}{8}$，由DM∥AB，推出∠B=∠MDC，∠MDC=∠C，CM=DM=$\frac{25}{8}$，FM=$\frac{15}{x}$-$\frac{25}{8}$，于DM∥AB，得$\frac{AO}{DM}$=$\frac{AF}{FM}$，代入化简即可．
（3）分三种情形讨论①当AO=AF时，②当FO=FA时，③当OA=OF时，分别计算即可．

解答 解：（1）∵AB=AC，
∴∠B=∠C，
∵∠EDC=∠B+∠BED，
∴∠FDC+∠EDO=∠B+∠BED，
∵∠EDO=∠B，
∴∠BED=∠EDC，
∵∠B=∠C，
∴△BDE∽△CFD．

（2）过点D作DM∥AB交AC于M（如图1中）．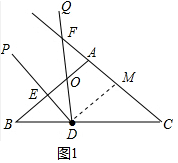

∵△BDE∽△CFD，
∴$\frac{CD}{BE}$=$\frac{FC}{BD}$，∵BC=8，BD=3，BE=x，
∴$\frac{FC}{3}$=$\frac{5}{x}$，
∴FC=$\frac{15}{x}$，
∵DM∥AB，
∴$\frac{DM}{AB}$=$\frac{CD}{CB}$，即$\frac{DM}{5}$=$\frac{5}{8}$，
∴DM=$\frac{25}{8}$，
∵DM∥AB，
∴∠B=∠MDC，
∴∠MDC=∠C，
∴CM=DM=$\frac{25}{8}$，FM=$\frac{15}{x}$-$\frac{25}{8}$，
∵DM∥AB，
∴$\frac{AO}{DM}$=$\frac{AF}{FM}$，即$\frac{y}{\frac{25}{8}}$=$\frac{\frac{15}{x}-5}{\frac{15}{x}-\frac{25}{8}}$，
∴y=$\frac{75-25x}{24-5x}$（0＜x＜3）．

（3）①当AO=AF时，
由（2）可知AO=y=$\frac{75-25x}{24-5x}$，AF=FC-AC=$\frac{15}{x}$-5，
∴$\frac{75-25x}{24-5x}$=$\frac{15}{x}$-5，解得x=$\frac{12}{5}$．
∴BE=$\frac{12}{5}$
②当FO=FA时，易知DO=AM=$\frac{15}{8}$，作DH⊥AB于H（如图2中），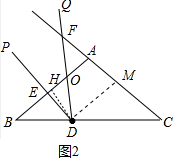

BH=BD•cos∠B=3×$\frac{4}{5}$=$\frac{12}{5}$，
DH=BD•sin∠B=3×$\frac{3}{5}$=$\frac{9}{5}$，
∴HO=$\sqrt{O{D}^{2}-D{H}^{2}}$=$\frac{21}{40}$，
∴OA=AB-BH-HO=$\frac{83}{40}$，
由（2）可知y=$\frac{75-25x}{24-5x}$，即$\frac{83}{40}$=$\frac{75-25x}{24-5x}$，解得x=$\frac{112}{65}$，
∴BE=$\frac{112}{65}$．
③当OA=OF时，设DP与CA的延长线交于点N（如图3中）．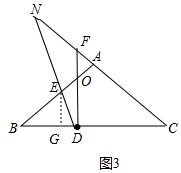

∴∠OAF=∠OFA，∠B=∠C=∠ANE，
由△ABC≌△CDN，可得CN=BC=8，ND=5，
由△BDE≌△NAE，可得NE=BE=x，ED=5-x，
作EG⊥BC于G，则BG=$\frac{4}{5}$x，EG=$\frac{3}{5}$x，
∴GD=$\sqrt{（5-x）^{2}-（\frac{3}{5}x）^{2}}$，
∴BG+GD=$\frac{4}{5}$x+$\sqrt{（5-x）^{2}-（\frac{3}{5}x）^{2}}$=3，
∴x=$\frac{40}{13}$＞3（舍弃），
综上所述，当△OAF是等腰三角形时，BE=$\frac{12}{5}$或$\frac{112}{65}$．

点评 本题考查相似三角形综合题、全等三角形的判定和性质、勾股定理、锐角三角函数、平行线分线段成比例定理等知识，解题的关键是灵活运用所学知识解决问题，学会利用参数解决问题，学会用分类讨论的思想思考问题，属于中考压轴题．