
【题目】直角三角形纸片ABC中,∠ACB=90°,AC≤BC,如图,将纸片沿某条直线折叠,使点A落在直角边BC上,记落点为D,设折痕与AB、AC边分别交于点E、F.
(1)如果∠AFE=65°,求∠CDF的度数;
(2)若折叠后的△CDF与△BDE均为等腰三角形,那么纸片中∠B的度数是多少?写出你的计算过程,并画出符合条件的折叠后的图形.

【答案】(1)40°;(2)45°或30°;图见解析;
【解析】
(1)根据翻折的性质,得到∠AFE=∠DFE=65°,即可求出∠CFD=180°﹣65°﹣65°=50°,根据直角三角形两个锐角互余的性质即可求出∠CDF的度数.
(2)先确定△CDF是等腰三角形,得出∠CFD=∠CDF=45°,因为不确定△BDE是以那两条边为腰的等腰三角形,故需讨论,①DE=DB,②BD=BE,③DE=BE,然后分别利用角的关系得出答案即可.
(1)根据翻折不变性可知:∠AFE=∠DFE=65°,
∴∠CFD=180°﹣65°﹣65°=50°,
∵∠C=90°,
∴∠CDF=90°﹣50°=40°.
(2)∵△CDF中,∠C=90°,且△CDF是等腰三角形,
∴CF=CD,
∴∠CFD=∠CDF=45°,
设∠DAE=x°,由对称性可知,AF=FD, AE=DE,
∴∠FDA=![]() ∠CFD=22.5°,∠DEB=2x°,
∠CFD=22.5°,∠DEB=2x°,
分类如下:
①当DE=DB时,∠B=∠DEB=2x°,
由∠CDE=∠DEB+∠B,得45°+22.5°+x=4x,
解得:x=22.5°.此时∠B=2x=45°;
见图形(1),说明:图中AD应平分∠CAB.
②当BD=BE时,则∠B=(180°﹣4x)°,
由∠CDE=∠DEB+∠B得:45°+22.5°+x=2x+180°﹣4x,
解得x=37.5°,此时∠B=(180﹣4x)°=30°.
图形(2)说明:∠CAB=60°,∠CAD=22.5°.
③DE=BE时,则![]()
由∠CDE=∠DEB+∠B得,45°+22.5°+x=2x+![]() ,
,
此方程无解.
∴DE=BE不成立.
综上所述:∠B=45°或30°.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=1,AC=2,现将△ABC绕点C顺时针旋转90°得到△A′B′C′,连接AB′,并有AB′=3,则∠A′的度数为( ) 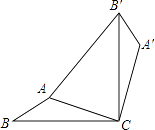
A.125°
B.130°
C.135°
D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】∠ACD是△ABC的外角,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.
(1)若∠A=58,求:∠E的度数.
(2)猜想∠A与∠E的关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)如图,已知△ABC,∠C=Rt∠,AC<BC,D为BC上一点,且到A,B两点的距离相等.

(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B=37°,求∠CAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某福利工厂准备在六一前夕准备生产甲、乙两种型号的玩具送给一所幼儿园,已知生产甲型玩具需要1号配件7个,2号配件2个;生产乙型玩具需要1号配件3个,2号配件5个,生产现有1号配件480个,2号配件370个,若该厂计划生产甲乙两种型号的玩具一共100个,用现有配件能否完成计划?如能,请写出所有的生产方案;如不能则说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名队员参加射击训练,成绩分别绘制成下列两个统计图:


根据以上信息,整理分析数据如下:
平均成绩(环) | 中位数(环) | 众数(环) | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击成绩,若选派其中一名参赛,你认为应选哪名队员?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com