
����Ŀ��ij�̵�Ҫ��һ��������üס����������ͣ�����������������12�˲�����ɣ���֧���˷ѹ�4800Ԫ�����ס�������������������������ҳ����������Ǽ׳���2������֪�ҳ������˷ѱȼ׳���200Ԫ��
��1���ֱ�����ס�������ÿ�˵��˷ѣ�
��2�����������ü׳��������������˶����ˣ�
��3����ͬʱ���üס�����������׳���x�ˣ��ҳ���y�ˣ�������������������x��y��Ϊ�������������˷�Ϊw��Ԫ������w��x�ĺ�����ϵʽ��ֱ��д��w����Сֵ��
���𰸡���1���ס�������ÿ�˵��˷ѷֱ�Ϊ300Ԫ��100Ԫ����2���������ü׳����������������18�ˣ���3��W��100x+3600��0��x��18����w����СֵΪ3700
��������
��1����ס�������ÿ�˵��˷ѷֱ�ΪmԪ��nԪ�����ݣ��ټ׳����é��ҳ����ã�200����12�����׳�����+�ҳ����ã���4800���з��������ɵã�
��2���赥�����ü׳����������������a�ˣ����ҳ����������������2a�ˣ����������������Ϊ1�����ݣ�12�����׳�ÿ��������+�ҳ�ÿ������������1���з�ʽ������⼴�ɣ�
��3���ȸ��ݣ��׳�x�˵�������+�ҳ�y�˵���������1�ɵ�y����x�ĺ�����ϵ���ٸ��ݣ����˷ѣ��׳������˷�+�ҳ������˷ѣ��г�W����x�ĺ�����ϵ����һ�κ��������ʿɵ�W����ֵ�����
�⣺��1����ס�������ÿ�˵��˷ѷֱ�ΪmԪ��nԪ��
��������ã�![]()
��ã�![]() ��
��
�𣺼ס�������ÿ�˵��˷ѷֱ�Ϊ300Ԫ��100Ԫ��
��2���赥�����ü׳����������������a�ˣ����ҳ����������������2a�ˣ�
��������ã�![]()
��ã�a��18��
������a��18��ԭ���̵Ľ⣬
�𣺵������ü׳����������������18�ˣ�
��3��������ã� ![]() ��
��
��y��36��2x
��W��300x+100y
��300x+100��36��2x��
��100x+3600��0��x��18����
��100��0��
��W����x�����������
��x��1ʱ��w����Сֵ��w����СֵΪ3700��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y��ax2+bx+c�IJ���ͼ����ͼ��������˵������abc��0����b+2a��0����b2��4ac����a+b+c����3����ȷ����(����)
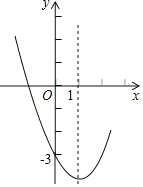
A.�٢�B.�٢ڢ�C.�٢ڢ�D.�٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
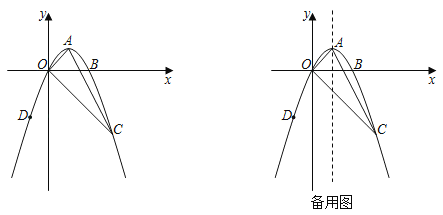
����Ŀ����֪������y��ax2+bx+c��x�ύ��O��B���㣬�䶥��A����Ϊ��1��1������CΪ�������ڵ��������ڵ�һ�㣬������Ϊ��3����3����
��1���������߽���ʽ��
��2����DΪ�������ڵ��������ڵ�һ�㣬����D��x�������߶Σ�����ΪH���Ƿ���ڵ�Dʹ�á�DHO���AOC���ƣ�������ڣ��������D���꣬��������ڣ���˵�����ɣ�
��3����E��F�ֱ�Ϊ�������Լ������߶Գ����ϵ������㣬�����Ƿ������BOΪ�ߣ�B��O��E��FΪ�����ƽ���ı��Σ����������ֱ��д����E���꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η��̣�x2����m��3��x��m=0��
��1�����ж�ԭ���̸��������
��2����������y=x2����m��3��x��m��x�ύ��A��x1��0����B��x2��0�����㣬��A��B�����ľ����Ƿ����������Сֵ�������ڣ�������ֵ���������ڣ���˵�����ɣ�
��������ʾ��AB=|x2��x1|��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����3�֣���ͬһƽ��ֱ������ϵ�У�����y=ax2+bx��y=bx+a��ͼ������ǣ� ��
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ÿ�����������ѧ�⣬������ͨ��һ����Ϸ����С�����������������һ�������ĺ����з������ſ�Ƭ��ÿ�ſ�Ƭ��д��һ��ʵ�����ֱ�Ϊ3��![]() ��2
��2![]() ��ÿ�ſ�Ƭ���������ʵ����ͬ�����������ͬ����������С����������ȡһ�ſ�Ƭ������鵽�Ŀ�Ƭ�ϵ�����������������С��ÿ�������ף�����Ͷ���ʮ�ף�
��ÿ�ſ�Ƭ���������ʵ����ͬ�����������ͬ����������С����������ȡһ�ſ�Ƭ������鵽�Ŀ�Ƭ�ϵ�����������������С��ÿ�������ף�����Ͷ���ʮ�ף�
��1������ֱ��д����������Ĺ���С��ÿ����������ѧ��ĸ��ʣ�
��2��С�������������Լ����Ϸ�����Լ��Ӻ����������ȡ���Σ�ÿ�γ�ȡһ�ſ�Ƭ����һ�γ�ȡ����¿�Ƭ�ϵ������ٽ���Ƭ�Żغ��г�ȡ�ڶ��Σ������ȡ������֮�������������Լ�ÿ����������ѧ�⣬����ÿ����ʮ�ף����б�������״ͼ���˹���С��ÿ����ʮ����ѧ��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2018�����ʡ�������ѧϰ��ѧ�����������¸߿����߿��������У�������߶������ش�仯��ij����Ϊ���˽����ߵ������������ij������ѧѧ������������������飬����ѧ�������ߵ��˽�̶��ɸߵ��ͷ�ΪA��B��C��D�ĸ��ȼ������Ե������������������������ͼ��������ͳ��ͼ���������ͼ���ṩ����Ϣ����������⣺
��1������ѧ������������������ͳ��ͼ����������
��2��������ͳ��ͼ�е�A�ȶ�Ӧ������Բ�ĽǵĶ�����
��3����֪��У��1500��ѧ�������Ƹ�Уѧ�������������˽�̶ȴﵽA�ȵ�ѧ���ж����ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
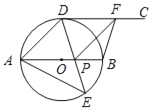
����Ŀ����ͼ��ABΪ��O��ֱ������D��E��λ��AB����İ�ԲAB�ϵĶ��㣬����DC����O�ڵ�D������DE��AE��DE��AB���ڵ�P��F������DC��һ���㣬����FP��FB���ҡ�AED��45�㣮
��1����֤��CD��AB��
��2����գ�
����DF��AP������DAE���� ��ʱ���ı���ADFP�����Σ�
����BF��DF������DAE���� ��ʱ���ı���BFDP�������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
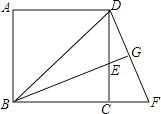
����Ŀ����ͼ����һ��������![]() ��С�����ӶԽ���
��С�����ӶԽ���![]() ����
����![]() ��ƽ���߽�
��ƽ���߽�![]() �ڵ�
�ڵ�![]() ���ֽ�
���ֽ�![]() �Ƶ�
�Ƶ�![]() ˳ʱ�뷽����ת
˳ʱ�뷽����ת![]() ��
��![]() ��λ�ã����ӳ�
��λ�ã����ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
��1����֤��![]() ��
��
��2����![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com