
【题目】经过三边都不相等的三角形的一个顶点的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
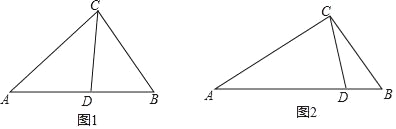
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线
(2)在△ABC中,∠A=52°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=3,BC=2,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
【答案】(1)详见解析;(2)∠ACB=96°或104°;(3)![]() .
.
【解析】试题分析:(1)根据完美分割线的定义只要证明①△ABC不是等腰三角形,②△ACD是等腰三角形,③△BDC∽△BCA即可.
(2)分三种情形讨论即可①如图2,当AD=CD时,②如图3中,当AD=AC时,③如图4中,当AC=CD时,分别求出∠ACB即可.
(3)设BD=x,利用△BCD∽△BAC,得![]() ,列出方程即可求出BD的长,然后再根据相似三角形的性质即可求出CD的长.
,列出方程即可求出BD的长,然后再根据相似三角形的性质即可求出CD的长.
试题解析:
(1)证明:如图1中,
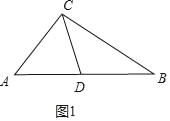
∵∠A=40°,∠B=60°,
∴∠ACB=80°,
∴△ABC不是等腰三角形,
∵CD平分∠ACB,
∴∠ACD=∠BCD=![]() ∠ACB=40°,
∠ACB=40°,
∴∠ACD=∠A=40°,
∴△ACD为等腰三角形,
∵∠DCB=∠A=40°,∠CBD=∠ABC,
∴△BCD∽△BAC,
∴CD是△ABC的完美分割线.
(2)①当AD=CD时,如图2,

∠ACD=∠A=52°,
∵△BDC∽△BCA,
∴∠BCD=∠A=52°,
∴∠ACB=∠ACD+∠BCD=104°.
②当AD=AC时,如图3中,
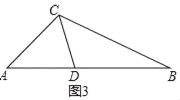
∠ACD=∠ADC=![]() =64°,
=64°,
∵△BDC∽△BCA,
∴∠BCD=∠A=52°,
∴∠ACB=∠ACD+∠BCD=116°.
③当AC=CD时,如图4中,

∠ADC=∠A=52°,
∵△BDC∽△BCA,
∴∠BCD=∠A=52°,
∴∠ADC=∠BCD
∵∠ADC>∠BCD,矛盾,舍弃.
综上所述,∠ACB=96°或104°.
(3)由已知AC=AD=3,
∵△BCD∽△BAC,
∴![]() =
=![]() ,设BD=x,
,设BD=x,
∴22=x(x+3),
∵x>0,
∴x=1,
∵△BCD∽△BAC,
∴![]() =
=![]() ,即
,即![]() ,
,
∴CD=![]() .
.


科目:初中数学 来源: 题型:
【题目】用A、B两种机器人搬运大米,A型机器人比B型机器人每小时多搬运20袋大米,A型机器人搬运700袋大米与B型机器人搬运500袋大米所用时间相等.求A、B型机器人每小时分别搬运多少袋大米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(类比学习)规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如4÷4÷4,(-2)÷(-2)÷(-2)÷(-2)÷(-2)等.类比有理数的乘方,我们把4÷4÷4记作![]() ,读作“4的3次除方”,(-2)÷(-2)÷(-2)÷(-2)÷(-2)记作
,读作“4的3次除方”,(-2)÷(-2)÷(-2)÷(-2)÷(-2)记作![]() ,读作“-2的5次除方”.
,读作“-2的5次除方”.
(探究活动)(1)直接写出计算结果:![]() = ;
= ;
(2)下列说法不正确的是( )
A.任何非零有理数的2次除方都等于1 B.负数的奇数次除方是负数
C.负数的偶数次除方是正数 D.3的2次除方等于2的3次除方
(深入思考)有理数的乘方运算可以转化为乘法运算,从而得出结果.那么有理数的除方运算与熟悉的运算一起,该如何进行?有理数的除方与有理数的乘方之间有何联系?
(3)计算:![]()
(4)直接写出2019与![]() 之间的关系:
之间的关系:
查看答案和解析>>
科目:初中数学 来源: 题型:
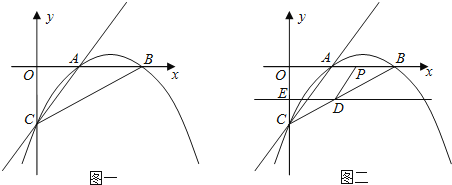
【题目】已知:如图一,抛物线![]() 与x轴正半轴交于A、B两点,与y轴交于点C,直线
与x轴正半轴交于A、B两点,与y轴交于点C,直线![]() 经过A、C两点,且
经过A、C两点,且![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移,且分别交y轴、线段BC于点E,D,同时动点P从点B出发,沿BO方向以每秒2个单位速度运动,
若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移,且分别交y轴、线段BC于点E,D,同时动点P从点B出发,沿BO方向以每秒2个单位速度运动,![]() 如图
如图![]() ;当点P运动到原点O时,直线DE与点P都停止运动,连DP,若点P运动时间为t秒;设
;当点P运动到原点O时,直线DE与点P都停止运动,连DP,若点P运动时间为t秒;设![]() ,当t为何值时,s有最小值,并求出最小值.
,当t为何值时,s有最小值,并求出最小值.
![]() 在
在![]() 的条件下,是否存在t的值,使以P、B、D为顶点的三角形与
的条件下,是否存在t的值,使以P、B、D为顶点的三角形与![]() 相似;若存在,求t的值;若不存在,请说明理由.
相似;若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(-1,0),B(3,0),将线段AB先向上平移![]() 个单位,再向右平移1个单位,得到线段CD,其中点A的对应点是点C.连接AC,BD,CD.
个单位,再向右平移1个单位,得到线段CD,其中点A的对应点是点C.连接AC,BD,CD.
(1)根据题意画出图形,直接写出C,D坐标;
(2)连接AD, 线段AD与![]() 轴交于点E,请用已经学过的知识求出E点的坐标(提示:请注意四边形ABDC的形状);
轴交于点E,请用已经学过的知识求出E点的坐标(提示:请注意四边形ABDC的形状);
(3)P(m,n)是坐标系内任一点,且![]() ,连接PC,PD,PO,PB,当
,连接PC,PD,PO,PB,当![]() ,
,![]() 时,这样的点P存在吗?有几个?并求出点P的坐标.
时,这样的点P存在吗?有几个?并求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班要在一面墙上同时展示数张形状、大小均相同的矩形绘画作品,将这些作品排成一个矩形(作品不完全重合).现需要在每张作品的四个角落都钉上图钉,如果作品有角落相邻,那么相邻的角落共享一枚图钉(例如用9枚图钉将4张作品钉在墙上如图).若有28枚图钉可供选用,则最多可以展示绘画作品( )
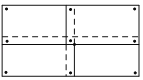
A. 16张B. 18张C. 20张D. 21张
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B两地相距120千米,甲乙两人沿同一条公路匀速行驶,甲骑自行车以20千米/时从A地前往B地,同时乙骑摩托车从B地前往A地,设两人之间的距离为s(千米),甲行驶的时间为t(小时),若s与t的函数关系如图所示,则下列说法错误的是( )

A.经过2小时两人相遇
B.若乙行驶的路程是甲的2倍,则t=3
C.当乙到达终点时,甲离终点还有60千米
D.若两人相距90千米,则t=0.5或t=4.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com