
����Ŀ�������ѧϰ���涨�������ɸ���ͬ������������������0���ij������������������4��4��4����-2������-2������-2������-2������-2����.����������ij˷������ǰ�4��4��4����![]() ��������4��3�γ���������-2������-2������-2������-2������-2������
��������4��3���������-2������-2������-2������-2������-2������![]() ��������-2��5�����.
��������-2��5�����.
��̽�������1��ֱ��д����������![]() = ��
= ��
��2������˵������ȷ���ǣ� ��
A���κη�����������2�γ���������1 B�������������γ����Ǹ���
C��������ż���γ��������� D��3��2�γ�������2��3�γ���
������˼�����������ij˷��������ת��Ϊ�˷����㣬�Ӷ��ó����.��ô�������ij�����������Ϥ������һ�𣬸���ν��У��������ij������������ij˷�֮���к���ϵ��
��3�����㣺![]()
��4��ֱ��д��2019��![]() ֮��Ĺ�ϵ��
֮��Ĺ�ϵ��
���𰸡���1��9����2��D��3��-8����4����Ϊ����
��������
��1���������е��¶�����㼴�����ֵ��
��2���������е��¶�����㼴�����ֵ��
��3����ԭʽ���μ��ɵõ������
��4����������ȷ�������ɣ�
�⣺��1��![]() =
=![]()
��2��A���κη�����������2�γ���������1 , ![]() ��ȷ
��ȷ
B�������������γ����Ǹ�������ȷ
C��������ż���γ�������������ȷ
D��3��2�������2��3�����![]() ������
������
��ѡD.
��3�����㣺![]()
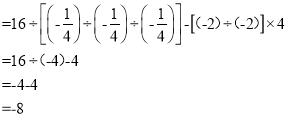
��4��������.


 ��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������Ŀ�Ľ�����̣�
��֪![]() Ϊ
Ϊ![]() �����ߣ�������
�����ߣ�������![]() �����ж�
�����ж�![]() ����״.
����״.
�⣺��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��ֱ��������
��ֱ��������
�ʣ���1������������̣�����һ����ʼ���ִ�����д���ò��Ĵ��ţ�����������
��2���ò���ȷ��д��Ӧ�ǣ�����������������������
��3��������ȷ�Ľ���Ϊ��������������������������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x�ķ�ʽ����![]() =1�Ľ�����������m��ȡֵ��Χ��_____��
=1�Ľ�����������m��ȡֵ��Χ��_____��
���𰸡�m��1
�����������������ȥ��ĸ�ã�2x��m��x��2��
��ã�x����m��2��
�߹���x�ķ���![]() ��1�Ľ���������
��1�Ľ���������
�࣭m��2��0��
���m����2��
�֡�x����m��2��2��
��m�٣�4��
��m��ȡֵ��Χ�ǣ�m����2��m�٣�4��
�ʴ�Ϊ��m����2��m�٣�4��
�㾦��������Ҫ�����˷�ʽ���̵Ľ⣬Ҫ�������գ�������Ĺؼ���Ҫ��ȷ���ڽⷽ�̵Ĺ�������Ϊ�ڰѷ�ʽ���̻�Ϊ��ʽ���̵Ĺ����У�������δ֪����ȡֵ��Χ�����ܲ������������������ĸ����0��ֵ������ԭ��ʽ���̵Ľ⣮
�����͡������
��������
18
����Ŀ��������x�ķ�ʽ���� ![]() �⣬��m��ֵΪ_______��
�⣬��m��ֵΪ_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ٹ�·����С�飬�˳��ض�����·Ѳ��ά�������Լ����Ϊ��������Ϊ�����������ʻ��¼����(��λ��ǧ��)����8����18����2����16����11����5.
(1)������С�����ĵط��ڳ�������ĸ�����������Զ��
(2)������������Ϊ0.8L��km����������������Ͷ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���糿��У������ҵ�������ʹ�绰�аְ���������ҵ�͵�ѧУ��С��Ҳͬʱ���Ҹϣ�����������С����ԭ�ٶȷ���ѧУ���ְ�����ԭ�ٶȵ�![]() ���ؼ�
���ؼ�![]() ��ְ����ߵ�ʱ��Ϊx���ӣ�С���Ͱְ�����֮��ľ���Ϊy�ף�y��x�ĺ�����ϵ��ͼ��ʾ����С���ص�ѧУʱ���ְֻ���Ҫ______���Ӳ��ܵ��ң�
��ְ����ߵ�ʱ��Ϊx���ӣ�С���Ͱְ�����֮��ľ���Ϊy�ף�y��x�ĺ�����ϵ��ͼ��ʾ����С���ص�ѧУʱ���ְֻ���Ҫ______���Ӳ��ܵ��ң�
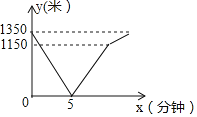
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y��ax2��bx��c��ͼ����ͼ��ʾ����P��|2a��b|��|3b��2c|��Q��|2a��b|��|3b��2c|�����ж�P��Q�Ĵ�С��ϵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ϵĵ�A��ʾ����Ϊ6����B��ʾ����Ϊ��4����C����A����B�ľ�����ȣ�����P�ӵ�B��������ÿ��2����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊx��x����0���룮
��1����C��ʾ�������� ����
��2����x=�� ����ʱ����P�����A����
��3���˶������е�P��ʾ�������� �����ú���ĸx��ʽ�ӱ�ʾ����
��4����P��C֮��ľ���Ϊ2����λ����ʱ����x��ֵ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������߶�����ȵ������ε�һ��������߶ΰ���������ηָ������С�����Σ�����ֵõ�����С��������һ��Ϊ���������Σ���һ����ԭ���������ƣ����ǰ������߶ν�����������ε������ָ��ߣ�
��1����ͼ1������ABC�У�CDΪ��ƽ���ߣ���A=40������B=60������֤��CDΪ��ABC�������ָ���
��2������ABC�У���A=52����CD����ABC�������ָ��ߣ�����ACDΪ���������Σ�����ACB�Ķ�����
��3����ͼ2����ABC�У�AC=3��BC=2��CD����ABC�������ָ��ߣ�����ACD����CDΪ�ױߵĵ��������Σ��������ָ���CD�ij���
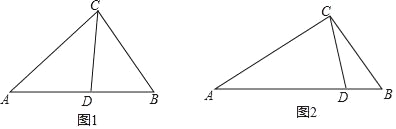
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��![]() ����
����![]() ��ֱ���ϵ����㣬
��ֱ���ϵ����㣬![]() ���ף���
���ף���![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() ���ף���
���ף���![]() ����
����![]() ��ֱ���ϵ��������㣬��
��ֱ���ϵ��������㣬��![]() ���ٶ�Ϊ1����/�룬��
���ٶ�Ϊ1����/�룬��![]() ���ٶ�Ϊ2����/�룬��
���ٶ�Ϊ2����/�룬��![]() �ֱ�ӵ�
�ֱ�ӵ�![]() ����
����![]() ͬʱ������ֱ�����˶�����������ʱ�߶�
ͬʱ������ֱ�����˶�����������ʱ�߶�![]() �ij�Ϊ5����.
�ij�Ϊ5����.
![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com