
����Ŀ����֪����ͼһ��������![]() ��x�������ύ��A��B���㣬��y�ύ�ڵ�C��ֱ��
��x�������ύ��A��B���㣬��y�ύ�ڵ�C��ֱ��![]() ����A��C���㣬��
����A��C���㣬��![]() ��
��
![]() �������ߵĽ���ʽ��
�������ߵĽ���ʽ��
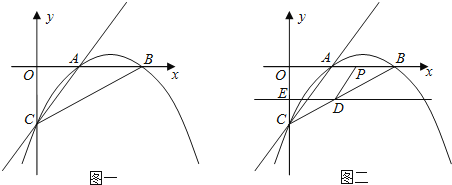
![]() ��ֱ��DEƽ����x�Ტ��C�㿪ʼ��ÿ��1����λ���ٶ���y��������ƽ�ƣ��ҷֱ�y�ᡢ�߶�BC�ڵ�E��D��ͬʱ����P�ӵ�B��������BO������ÿ��2����λ�ٶ��˶���
��ֱ��DEƽ����x�Ტ��C�㿪ʼ��ÿ��1����λ���ٶ���y��������ƽ�ƣ��ҷֱ�y�ᡢ�߶�BC�ڵ�E��D��ͬʱ����P�ӵ�B��������BO������ÿ��2����λ�ٶ��˶���![]() ��ͼ
��ͼ![]() ������P�˶���ԭ��Oʱ��ֱ��DE���P��ֹͣ�˶�����DP������P�˶�ʱ��Ϊt�룻��
������P�˶���ԭ��Oʱ��ֱ��DE���P��ֹͣ�˶�����DP������P�˶�ʱ��Ϊt�룻��![]() ����tΪ��ֵʱ��s����Сֵ���������Сֵ��
����tΪ��ֵʱ��s����Сֵ���������Сֵ��
![]() ��
��![]() �������£��Ƿ����t��ֵ��ʹ��P��B��DΪ�������������
�������£��Ƿ����t��ֵ��ʹ��P��B��DΪ�������������![]() ���ƣ������ڣ���t��ֵ���������ڣ���˵�����ɣ�
���ƣ������ڣ���t��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��y=![]() ��(2)
��(2)![]() ʱ��s����Сֵ������СֵΪ1��(3)
ʱ��s����Сֵ������СֵΪ1��(3)![]() ��
��![]() .
.
��������������
��1���������õ�A��B��C������ֱ�Ϊ��2��0������4��0���ͣ�0��-2�������ô���ϵ������������ߵĽ���ʽ���ɣ�
��2���ɣ�1�������õ�A��B��C������ɵ�OB=4��OC=2���ɴ˿ɵ�tan��OCB=2�����CE=t���ɵ�DE=2t�����OP=OB-PB=4-2t�����ú�t�Ĵ���ʽ�����S����϶��κ��������ʼ������tΪ��ֵʱ��S��С����Сֵ�Ƕ����ˣ�
��3����OB=5��OC=2��BC=![]() ����EC=t��DE=2t��CD=
����EC=t��DE=2t��CD=![]() ���Ӷ��ɵ�BD=
���Ӷ��ɵ�BD=![]() ������ABC=��PBD��֪��t��ֵ����
������ABC=��PBD��֪��t��ֵ����![]() ��
��![]() ʱ�������������ƽ��м������ۼ�����ö�Ӧ��t��ֵ.
ʱ�������������ƽ��м������ۼ�����ö�Ӧ��t��ֵ.
��⣺
![]() ��ֱ�ߣ�
��ֱ�ߣ�![]() ֪��
֪��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ����
����![]() ��
��
�������ߵĽ���ʽΪ��![]() ������
������![]() ���ã�
���ã�
![]() �����
�����![]()
�������ߵĽ���ʽ��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
�൱![]() ʱ��s����Сֵ������СֵΪ1��
ʱ��s����Сֵ������СֵΪ1��
![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��
��![]() ��
��
��P��B��DΪ�������������![]() ���ƣ���֪
���ƣ���֪![]() ���������������
���������������
![]() �����
�����![]() ��
��
![]() �����
�����![]() ��
��
���ϣ���![]() ��
��![]() ʱ����P��B��DΪ�������������
ʱ����P��B��DΪ�������������![]() ���ƣ�
���ƣ�


 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
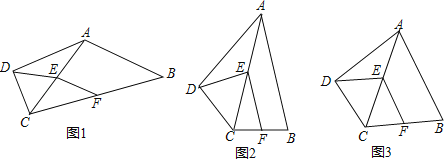
����Ŀ����ͼ1�����ı���ABCD�У���ADC��90�㣬AB��AC����E��F�ֱ�ΪAC��BC���е㣬����EF��DE��
��1������ͼ1���ҳ�������ȵ������߶Σ���˵�����ɣ���AB��AC���⣩
��2����ͼ2����ACƽ�֡�BAD����DEF��90��ʱ�����BAD�Ķ�����
��3����ͼ3���ı���CDEF�DZ߳�Ϊ2�����Σ���S�ı���ABCD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ٹ�·����С�飬�˳��ض�����·Ѳ��ά�������Լ����Ϊ��������Ϊ�����������ʻ��¼����(��λ��ǧ��)����8����18����2����16����11����5.
(1)������С�����ĵط��ڳ�������ĸ�����������Զ��
(2)������������Ϊ0.8L��km����������������Ͷ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y��ax2��bx��c��ͼ����ͼ��ʾ����P��|2a��b|��|3b��2c|��Q��|2a��b|��|3b��2c|�����ж�P��Q�Ĵ�С��ϵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ϵĵ�A��ʾ����Ϊ6����B��ʾ����Ϊ��4����C����A����B�ľ�����ȣ�����P�ӵ�B��������ÿ��2����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊx��x����0���룮
��1����C��ʾ�������� ����
��2����x=�� ����ʱ����P�����A����
��3���˶������е�P��ʾ�������� �����ú���ĸx��ʽ�ӱ�ʾ����
��4����P��C֮��ľ���Ϊ2����λ����ʱ����x��ֵ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() �Ľ�������ʽΪ
�Ľ�������ʽΪ![]() ����
����![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��ֱ��
��ֱ��![]() ������
������![]() ��ֱ��
��ֱ��![]() ��
�� ![]() ���ڵ�
���ڵ�![]() ��
��

��1�����![]() �����ꣻ
�����ꣻ
��2����ֱ��![]() �Ľ�������ʽ��
�Ľ�������ʽ��
��3����![]() �������
�������
��4����ֱ��![]() �ϴ������ڵ�
�ϴ������ڵ�![]() ����һ��
����һ��![]() ��ʹ��
��ʹ��![]() ��
��![]() �������ȣ���ֱ��д����
�������ȣ���ֱ��д����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������߶�����ȵ������ε�һ��������߶ΰ���������ηָ������С�����Σ�����ֵõ�����С��������һ��Ϊ���������Σ���һ����ԭ���������ƣ����ǰ������߶ν�����������ε������ָ��ߣ�
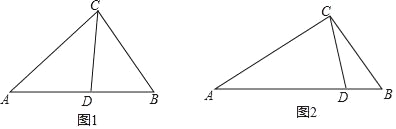
��1����ͼ1������ABC�У�CDΪ��ƽ���ߣ���A=40������B=60������֤��CDΪ��ABC�������ָ���
��2������ABC�У���A=52����CD����ABC�������ָ��ߣ�����ACDΪ���������Σ�����ACB�Ķ�����
��3����ͼ2����ABC�У�AC=3��BC=2��CD����ABC�������ָ��ߣ�����ACD����CDΪ�ױߵĵ��������Σ��������ָ���CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��MON=25��������ABCD�ı�BC��OM�ϣ��Խ���AC��ON��
��1�����ACD������
��2����AC=5ʱ����AD�ij������ο����ݣ�sin25��=0.42��cos25��=0.91��tan25��=0.47�������ȷ��0.1��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����и�ʽ��
![]()
![]()
![]()
����
������Ĺ��ɣ�
��1����![]() ��ֵ��
��ֵ��
��2����![]() ��+2+1�ĸ�λ���֣�
��+2+1�ĸ�λ���֣�
��3�������������������![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com