
【题目】如图,一次函数的图象与反比例函数的图象交于A、B两点.
(1)利用图中的条件,求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)根据图象直接写出使一次函数的值小于反比例函数的值的x的取值范围.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知AB=24cm,CD=8cm.
(1)求作此残片所在的圆(不写作法,保留作图痕迹)
(2)求残片所在圆的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】未来五年,国家将投入8500亿元用于缓解群众“看病难,看病贵”问题.将8500亿元用科学记数法表示为 ( )元
A.0.85×1012
B.8.5×1011
C.8.5×1012
D.85×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论:
①b2﹣4ac<0;②abc>0;③a﹣b+c<0;④m>﹣2,
其中,正确的个数有( )
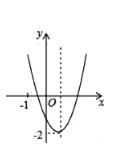
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 的函数表达式为
的函数表达式为![]() ,它与
,它与![]() 轴、
轴、![]() 轴的交点分别为A、B两点.
轴的交点分别为A、B两点.
(1)求点A、B的坐标;
(2)设F是![]() 轴上一动点,⊙P经过点B且与
轴上一动点,⊙P经过点B且与![]() 轴相切于点F,设⊙P的圆心坐标为P(x,y),求y与
轴相切于点F,设⊙P的圆心坐标为P(x,y),求y与![]() 之间的函数关系;
之间的函数关系;
(3)是否存在这样的⊙P,既与![]() 轴相切,又与直线
轴相切,又与直线![]() 相切于点B?若存在,求出圆心P的坐标;若不存在,请说明理由.
相切于点B?若存在,求出圆心P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.

(1)求∠ABC的度数;
(2)求证:AE是⊙O的切线;
(3)当BC=4时,求劣弧AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度约为( )(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)
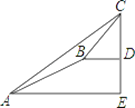
A. 8.1米 B. 17.2米 C. 19.7米 D. 25.5米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com