
【题目】如图,已知直线![]() 的函数表达式为
的函数表达式为![]() ,它与
,它与![]() 轴、
轴、![]() 轴的交点分别为A、B两点.
轴的交点分别为A、B两点.
(1)求点A、B的坐标;
(2)设F是![]() 轴上一动点,⊙P经过点B且与
轴上一动点,⊙P经过点B且与![]() 轴相切于点F,设⊙P的圆心坐标为P(x,y),求y与
轴相切于点F,设⊙P的圆心坐标为P(x,y),求y与![]() 之间的函数关系;
之间的函数关系;
(3)是否存在这样的⊙P,既与![]() 轴相切,又与直线
轴相切,又与直线![]() 相切于点B?若存在,求出圆心P的坐标;若不存在,请说明理由.
相切于点B?若存在,求出圆心P的坐标;若不存在,请说明理由.

【答案】(1)A(﹣4,0),B(0,3); (2)y=![]() x2+
x2+![]() ; (3)存在.点
; (3)存在.点![]() 的坐标为(1,
的坐标为(1, ![]() )或(﹣9,15).
)或(﹣9,15).
【解析】试题分析:(1)根据坐标轴上点的坐标特征易得以A点坐标为(﹣4,0), B点坐标为(0,3),
(2)过点P作PD⊥y轴于D,则PD=![]() ,BD=
,BD=![]() ,根据切线的性质得PF=y,则PB=y,
,根据切线的性质得PF=y,则PB=y,
在Rt△BDP中,根据勾股定理得到y2=x2+(3﹣y)2 ,然后整理可得到:y=![]() x2+
x2+![]() ,
,
(3)因为⊙P与![]() 轴相切于点F,且与直线
轴相切于点F,且与直线![]() 相切于点B,根据切线长定理得到:AB=AF,而AB=5,所以AF=
相切于点B,根据切线长定理得到:AB=AF,而AB=5,所以AF=![]() 再把
再把![]() 分别代入y=
分别代入y=![]() x2+
x2+![]() 计算出对应的函数值,即可确定P点坐标.
计算出对应的函数值,即可确定P点坐标.
试题解析:(1)A点坐标为(﹣4,0),B点坐标为(0,3),
(2)过点P作PD⊥y轴于D,如图1,

则PD=|x|,BD=|3﹣y|,
∵⊙P经过点B且与x轴相切于点F,
∴PB=PF=y,
在Rt△BDP中,
∴PB2=PD2+BD2,
∴y2=x2+(3﹣y)2,
∴y=![]() x2+
x2+![]() ,
,
(3)存在.
如图2,∵⊙P与x轴相切于点F,且与直线l相切于点B,
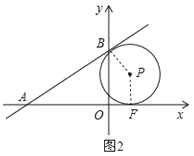
∴AB=AF,
∵AB2=OA2+OB2=52,
∴AF=5,
∵AF=|x+4|,
∴|x+4|=5,
∴x=1或x=﹣9,
当x=1时,y=![]() ,
,
当x=﹣9时,y=![]() =15,
=15,
∴点![]() 的坐标为(1,
的坐标为(1, ![]() )或(﹣9,15).
)或(﹣9,15).


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
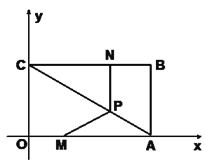
【题目】(本小题满分12分)如图,在平面直角坐标系中,矩形ABCO的OA边在![]() 轴上,OC边在
轴上,OC边在![]() 轴上,且B点坐标为(4,3).动点M、N分别从点O、B同时出发,以1单位/秒的速度运动(点M沿OA向终点A运动,点N沿BC向终点C运动),过点N作NP∥AB交AC于点P,连结MP.
轴上,且B点坐标为(4,3).动点M、N分别从点O、B同时出发,以1单位/秒的速度运动(点M沿OA向终点A运动,点N沿BC向终点C运动),过点N作NP∥AB交AC于点P,连结MP.
(1)直接写出OA、AB的长度;
(2)试说明△CPN∽△CAB;
(3)在两点的运动过程中,请求出ΔMPA的面积S与运动时间![]() 的函数关系式;
的函数关系式;
(4)在运动过程中,△MPA的面积S是否存在最大值?若存在,请求出当![]() 为何值时有最大值,并求出最大值;若不存在,请说明理由.
为何值时有最大值,并求出最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面不是平行线的判定定理的是( )
A. 在同一平面内,没有公共点的两条直线叫做平行线
B. 同位角相等,两直线平行
C. 内错角相等,两直线平行
D. 同旁内角互补,两直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数的图象与反比例函数的图象交于A、B两点.
(1)利用图中的条件,求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)根据图象直接写出使一次函数的值小于反比例函数的值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①同位角相等;②对顶角相等;③等角的补角相等;④两直线平行,同旁内角相等,正确的个数有( )
A. 1 个B. 2 个C. 3 个D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平行四边形ABCD,下列条件中,不能判定这个平行四边形为矩形的是( )
A. ∠A=∠B B. ∠A=∠C C. AC=BD D. AB⊥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)株洲五桥主桥主孔为拱梁钢构组合体系(如图1),小明暑假旅游时,来到五桥观光,发现拱梁的路面部分有均匀排列着9根支柱,他回家上网查到了拱梁是抛物线,其跨度为20米,拱高(中柱)10米,于是他建立如图2的坐标系,发现可以将余下的8根支柱的高度都算出来了,请你求出中柱左边第二根支柱CD的高度.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com