
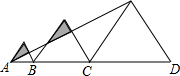
 已知三个边长分别为2、3、5的正三角形从左到右如图排列,则图中阴影部分面积为
已知三个边长分别为2、3、5的正三角形从左到右如图排列,则图中阴影部分面积为| 1 |
| 2 |
| ||
| 2 |
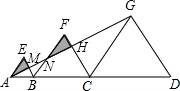 解:
解:| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 8 |
| ||
| 2 |
| ||
| 8 |
5
| ||
| 8 |
5
| ||
| 8 |


科目:初中数学 来源: 题型:
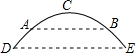 如图是某地一座抛物线形拱桥,桥拱在竖直平面内,与水面相交于A,B两点,拱桥最高点C到AB的距离为9m,AB=36m,D,E为拱桥底部的两点,且DE∥AB,点E到直线AB的距离为7m.建立平面直角坐标系,求:
如图是某地一座抛物线形拱桥,桥拱在竖直平面内,与水面相交于A,B两点,拱桥最高点C到AB的距离为9m,AB=36m,D,E为拱桥底部的两点,且DE∥AB,点E到直线AB的距离为7m.建立平面直角坐标系,求:查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
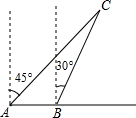 如图所示,一渔船正以每小时30海里的速度由西向东航行,在A处看见小岛C在船的北偏东45°方向上.40min后,渔船行至B处,此时看见小岛C在船的北偏东30°.若以小岛C为中心周围30海里是危险区,问这艘渔船继续向东航行是否有进入危险区的可能?
如图所示,一渔船正以每小时30海里的速度由西向东航行,在A处看见小岛C在船的北偏东45°方向上.40min后,渔船行至B处,此时看见小岛C在船的北偏东30°.若以小岛C为中心周围30海里是危险区,问这艘渔船继续向东航行是否有进入危险区的可能?查看答案和解析>>
科目:初中数学 来源: 题型:
| A、两点之间,线段最短 |
| B、过不在同一直线上的三点有且只有一个圆 |
| C、一组对应边相等的两个等边三角形全等 |
| D、对角线相等的四边形是矩形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com