
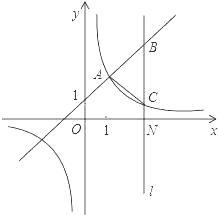
【题目】如图,一次函数y=kx+1(k≠0)与反比例函数y=![]() (m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积?
【答案】(1)一次函数解析式为y=x+1;反比例解析式为y=![]() ;(2)
;(2)![]() .
.
【解析】(1)将A坐标代入一次函数解析式中求出k的值,确定出一次函数解析式,将A坐标代入反比例函数解析式中求出m的值,即可确定出反比例解析式;
(2)设一次函数与x轴交点为D点,过A作AE垂直于x轴于E,三角形ABC面积=三角形BDN面积-三角形ADE面积-梯形AECN面积,求出即可.
(1)将A(1,2)代入一次函数解析式得:k+1=2,即k=1,
∴一次函数解析式为y=x+1;
将A(1,2)代入反比例解析式得:m=2,
∴反比例解析式为y=![]() ;
;
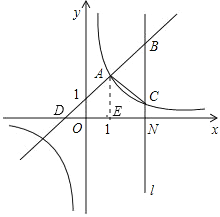
(2)设一次函数与x轴交于D点,过A作AE垂直于x轴于E,令y=0,求出x=-1,即OD=1,
∵A(1,2),
∴AE=2,OE=1,
∵直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
∴点B、C的横坐标为3,
将x=3代入一次函数得:y=4,将x=3代入反比例解析式得:y=![]() ,
,
∴B(3,4),即ON=3,BN=4,C(3,![]() ),即CN=
),即CN=![]() ,
,
则S△ABC=S△BDN-S△ADE-S梯形AECN=![]() ×4×4-
×4×4-![]() ×2×2-
×2×2-![]() ×(
×(![]() +2)×2=
+2)×2=![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
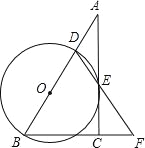
【题目】在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O交AC于点E,连结DE并延长,与BC的延长线交于点F.且BD=BF.
(1)求证:AC与⊙O相切.
(2)若BC=6,AB=12,求⊙O的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中装有8个红球和16个白球,它们除颜色不同外其余都相同.
(1)求从布袋中摸出一个球是红球的概率;
(2)现从布袋中取走若干个白球,并放入相同数目的红球,搅拌均匀后,再从布袋中摸出一个球是红球的概率是![]() ,问取走了多少个白球?
,问取走了多少个白球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一元二次方程ax2+bx+c=0有一个根为﹣1,则下列等式成立的是( )
A. a+b+c=1 B. a﹣b+c=0 C. a+b+c=0 D. a﹣b+c=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 棱柱的侧面可以是三角形 B. 棱柱的各条棱都相等
C. 正方体的各条棱都相等 D. 六个大小一样的正方形所拼成的图形是正方体的表面展开图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式从左到右的变形错误的是 ( )
A.y-x = x-yB.-a-b=-(a+b)
C.(y-x)2=(x-y)2D.(a-b)3=-(b-a)3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将△ABC的三个顶点的纵坐标保持不变,横坐标分别乘以-1,依次连接新的这些点,则所得三角形与原三角形的位置关系是( )
A. 原三角形向x轴的负方向平移一个单位即为所得三角形
B. 关于原点对称
C. 关于x轴对称
D. 关于y轴对称
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com