
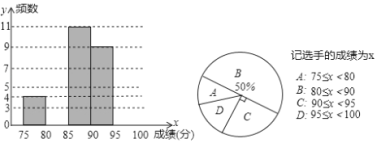
【题目】胜利中学为丰富同学们的校园生活,举行“校园电视台主持人”选拔赛,现将36名参赛选手的成绩(单位:分)统计并绘制成频数分布直方图和扇形统计图,部分信息如下:
请根据统计图的信息,解答下列问题:
(1)补全频数分布直方图.
(2)扇形统计图中扇形A对应的圆心角度数为 ;
(3)成绩在D区域的选手,男生比女生多一人,从中随机抽取两人临时担任该校艺术节的主持人,求恰好选中一名男生和一名女生的概率.
【答案】(1)见解析; (2) 40![]() ;(3)
;(3)![]()
【解析】
(1)由![]() 组百分比求得其人数,据此可得80~85的频数,再根据各组频数之和等于总人数可得最后一组频数,从而补全图形,
组百分比求得其人数,据此可得80~85的频数,再根据各组频数之和等于总人数可得最后一组频数,从而补全图形,
(2)先求出A的人数所占的百分比,然后再用![]() 乘以这个百分比即可得答案;
乘以这个百分比即可得答案;
(3)画树状图展示所有等可能的结果数,找出抽取的学生恰好是一名男生和一名女生的结果数,然后根据概率公式求解.
解:(1)80~90的频数为![]() ,则80~85的频数为
,则80~85的频数为![]() ,95~100的频数为
,95~100的频数为![]() ,
,
补全图形如下:
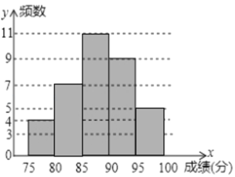
(2)扇形统计图中扇形![]() 对应的圆心角度数为
对应的圆心角度数为![]() ;
;
(3)∵成绩在![]() 区域的选手共有5人,男生比女生多1人,
区域的选手共有5人,男生比女生多1人,
∴男生有3人,女生有2人.
画树状图为:
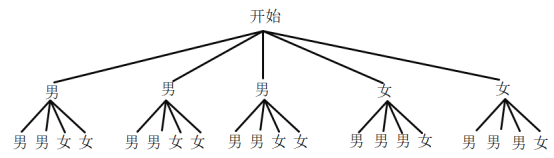
共有20种等可能的结果数,其中抽取的学生恰好是一名男生和一名女生的结果数为12,
所以抽取的学生恰好是一名男生和一名女生的概率为![]() .
.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以BC为直径的⊙O交AC于点E,过点E作AB的垂线交AB于点F,交CB的延长线于点G,且∠ABG=2∠C.
(1)求证:EG是⊙O的切线;
(2)若tanC=![]() ,AC=8,求⊙O的半径.
,AC=8,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点.请你添加一个条件,使四边形EFGH为矩形,应添加的条件是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是为(0,3)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.

(1)若抛物线过点C、A、A′,求此抛物线的解析式;
(2)求平行四边形ABOC和平行四边形A′B′OC′重叠部分△OC′D的周长;
(3)点M是第一象限内抛物线上的一动点,问:点M在何处时;△AMA′的面积最大?最大面积是多少?并求出此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
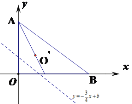
【题目】如图,在平面直角坐标系中,已知点A坐标(0,3),点B坐标(4,0),将点O沿直线![]() 对折,点O恰好落在∠OAB的平分线上的O’处,则
对折,点O恰好落在∠OAB的平分线上的O’处,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学团委组织征文活动,并设立若干奖项.学校计划派人根据设奖情况去购买![]() 三种奖品共
三种奖品共![]() 件,其中
件,其中![]() 型奖品件数比
型奖品件数比![]() 型奖品件数的
型奖品件数的![]() 倍少
倍少![]() 件,
件,![]() 型奖品所花费用不超过
型奖品所花费用不超过![]() 型奖品所花费用的
型奖品所花费用的![]() 倍.各种奖品的单价如右表所示.如果计划
倍.各种奖品的单价如右表所示.如果计划![]() 型奖品买
型奖品买![]() 件,买
件,买![]() 件奖品的总费用是
件奖品的总费用是![]() 元.
元.
|
|
| |
单价(元) |
|
|
|
(1)试求![]() 与
与![]() 之间的函数关系式,并求出自变量
之间的函数关系式,并求出自变量![]() 的取值范围;
的取值范围;
(2)请你设计一种方案,使得购买这三种奖品所花的总费用最少,并求出最少费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古代有着辉煌的数学成就,《周髀算经》,《九章算术》,《海岛算经》,《孙子算经》等是我国古代数学的重要文献.
(1)小聪想从这4部数学名著中随机选择1部阅读,则他选中《九章算术》的概率为 ;
(2)某中学拟从这4部数学名著中选择2部作为“数学文化”校本课程学习内容,求恰好选中《九章算术》和《孙子算经》的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市绿化工程进行招标,现有甲、乙两个工程队投标,已知甲队单独完成这项工程需要60天.经测算:如果甲队先做20天,再由甲队、乙队合作12天,那么此时共完成总工作量的![]() .
.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天需付工程款4.5万元,乙队施工一天需付工程款2万元,该工程由甲乙两队合作若干天后,再由乙队完成剩余的工作,若要求完成此项工程的工程款不超过186万元,求甲、乙两队最多合作多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com