
【题目】已知平行四边形ABCD中,对角线AC、BD相交于O.则下列说法准确的是( )
A.当![]() 时,平行四边形ABCD为矩形
时,平行四边形ABCD为矩形
B.当![]() 时,平行四边形ABCD为正方形
时,平行四边形ABCD为正方形
C.当![]() 时,平行四边形ABCD为菱形
时,平行四边形ABCD为菱形
D.当![]() 时,平行四边形ABCD为菱形
时,平行四边形ABCD为菱形
【答案】D
【解析】
A. 根据平行四边形的性质和对角线相等的平行四边形是矩形进行判断;
B. 根据邻边相等的平行四边形是菱形进行判断;
C. 根据有一个角是直角的平行四边形是矩形进行判断;
D. 根据对角线互相垂直的平行四边形是菱形进行判断.
∵平行四边形对角线互相平分,
∴OA=OC
而对角线相等的平行四边形是矩形,
∴OA=OC不能判定平行四边形ABCD为矩形,故A错误;
∵邻边相等的平行四边形是菱形,
∴当![]() 时,平行四边形ABCD是菱形,故B错误;
时,平行四边形ABCD是菱形,故B错误;
∵有一个角是直角的平行四边形是矩形
∴当![]() 时,平行四边形ABCD为矩形,故C错误;
时,平行四边形ABCD为矩形,故C错误;
∵对角线互相垂直的平行四边形是菱形
∴当![]() 时,平行四边形ABCD为菱形,故D正确.
时,平行四边形ABCD为菱形,故D正确.
故选D.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】山西是我国酿酒最早的地区之一,山西酿酒业迄今为止已有![]() 余年的历史.在漫长的历史进程中,山西人民酿造出品种繁多、驰名中外的美酒佳酿,其中以汾酒、竹叶青酒最为有名.某烟酒超市卖有竹叶青酒,每瓶成本价是
余年的历史.在漫长的历史进程中,山西人民酿造出品种繁多、驰名中外的美酒佳酿,其中以汾酒、竹叶青酒最为有名.某烟酒超市卖有竹叶青酒,每瓶成本价是![]() 元,经调查发现,当售价为
元,经调查发现,当售价为![]() 元时,每天可以售出
元时,每天可以售出![]() 瓶,售价每降低
瓶,售价每降低![]() 元,可多售出
元,可多售出![]() 瓶(售价不高于
瓶(售价不高于![]() 元)
元)
(1)售价为多少时可以使每天的利润最大?最大利润是多少?
(2)要使每天的利润不低于![]() 元,每瓶竹叶青酒的售价应该控制在什么范围内?
元,每瓶竹叶青酒的售价应该控制在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
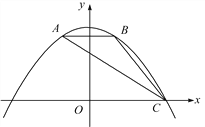
【题目】如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0, ![]() ),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
),点A坐标为(-1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
(1)求该抛物线的函数解析式;
(2)点F为线段AC上一动点,过点F作FE⊥x轴,FG⊥y轴,垂足分别为点E,G,当四边形OEFG为正方形时,求出点F的坐标;
(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动,设平移的距离为t,正方形的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线L:y=ax2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1.
(1)求抛物线L的解析式;
(2)将抛物线L向下平移h个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求h的取值范围;
(3)设点P是抛物线L上任一点,点Q在直线l:x=﹣3上,△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能,求出符合条件的点P的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮正在参加学校举办的古诗词比赛节目,他须答对两道单选题才能顺利通过最后一关,其中第一题有A、B、C、D共4个选项,第二题有A、B、C共3个选项,而这两题小亮都不会,但小亮有一次使用“特权”的机会(使用“特权”可去掉其中一题的一个错误选项).
(1)如果小亮第一题不使用“特权”,随机选择一个选项,那么小亮答对第一题的概率是________.
(2)如果小亮将“特权”留在第二题,请用画树状图或列表法来求出小亮通过最后一关的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤.通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤.为保证每天至少售出260斤,张阿姨决定降价销售.
销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元.为扩大销售,增加盈利,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.
(1)每件衬衫降价多少元时,商场平均每天的盈利是1050元?
(2)每件衬衫降价多少元时,商场平均每天盈利最大?最大盈利是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地要建一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子OA,O恰在水面中心,安装在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下.如图建立平面直角坐标系,已知A(![]() ),顶点P(
),顶点P(![]() )
)
(1) 求抛物线的解析式
(2) 若不计其他因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外

查看答案和解析>>
科目:初中数学 来源: 题型:
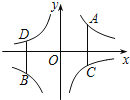
【题目】如图,已知点A、B在双曲线y=![]() (m>0)上,点C、D在双曲线y=
(m>0)上,点C、D在双曲线y=![]() (n<0)上,AC∥BD∥y轴,AC=3,BD=4,AC与BD的距离为7,则m﹣n的值为_____.
(n<0)上,AC∥BD∥y轴,AC=3,BD=4,AC与BD的距离为7,则m﹣n的值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com