Question

【题目】如图，正方形BCPQ对角线交于点A，将一块等腰直角三角形中45°角的顶点放在A点，斜边AG所在的直线交BC于点D，直角边AH所在的直角交BC于点E．
（1）在边BC上取一点M，连接AM，AD平分∠BAM，求证：AE平分∠MAC；
（2）在（1）的条件下，请判断BD、CE、DE之间的数量关系，并证明你的结论．

Answer 1

【答案】
（1）证明：∵∠DAE=45°，

∴∠DAM+∠EAM=45°，

在正方形BCPQ中，BP⊥CQ，∴∠BAC=90°，

∴∠BAD+∠CAE=45°，

∴∠DAM+∠EAM=∠BAD+∠EAC

AD平分∠BAM，

∴∠BAD=∠DAM

∴∠EAM=∠EAC 即AE平分∠MAC．

（2）解：结论：BD2+CE2=DE2．

证明：延长AM到点F，使AF=AB，

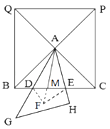
在正方形BCPQ中，AB=AC，∠BAC=90°，

∴AF=AC，∠ABC=∠ACB=45°，

∵∠BAD=∠DAM 由（1）知，∠EAM=∠EAC，

又AF=AF，

∴△FAD≌△BAD，△FAE≌△CAE，

∴∠AFD=∠ABC=45°，DF=BD，∠AFE=∠ACB=45°，EF=EC，

∴∠DFE=90°，

在Rt△DEF中，DF2+EF2=DE2，

∴BD2+CE2=DE2．

【解析】（1）只要证明∠DAM+∠EAM=∠BAD+∠EAC，由AD平分∠BAM，可得∠BAD=∠DAM即可推出∠EAM=∠EAC．
【考点精析】认真审题，首先需要了解等腰直角三角形(等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°)，还要掌握正方形的性质(正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形)的相关知识才是答题的关键．