
分析 先根据题意画出图形,再根据正六边形的性质求出∠BOC的度数,判断出△BOC为等边三角形即可求出答案.
解答 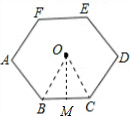 解:如图所示,连接OB、OC;
解:如图所示,连接OB、OC;
∵此六边形是正六边形,
∴∠BOC=360°÷6=60°,
∵OB=OC,
∴△BOC是等边三角形,
∴OB=OC=BC=6.
作OM⊥BC于M点,
∴∠BOM=$\frac{1}{2}$∠BOC=30°,
∴OM=OB•cos30°=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$.
∴正六边形的面积=6S△BOC=6×$\frac{1}{2}$×6×3$\sqrt{3}$=54$\sqrt{3}$.
故答案为:6,3$\sqrt{3}$,54$\sqrt{3}$.
点评 本题考查了正多边形与圆的知识,解答此题的关键是根据题意画出图形,作出辅助线;由正六边形的性质判断出△BOC的形状是解答此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | x<$\frac{1}{3}$ | B. | x>$\frac{1}{3}$ | C. | x<0 | D. | x>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
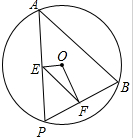 如图,点A,B是⊙O上两点,点P是⊙O0上的动点(P与A,B不重合),连接AP,BP,过点O分别作OE⊥AP,OF⊥BP,点E、F分别是垂足.
如图,点A,B是⊙O上两点,点P是⊙O0上的动点(P与A,B不重合),连接AP,BP,过点O分别作OE⊥AP,OF⊥BP,点E、F分别是垂足.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
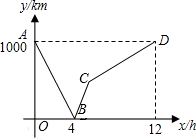 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.下列说法中正确的是③.
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.下列说法中正确的是③.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com