
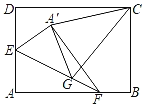
【题目】如图,在矩形纸片ABCD中,AB=8,BC=6,点E是AD的中点,点F是AB上一动点.将△AEF沿直线EF折叠,点A落在点A'处.在EF上任取一点G,连接GC,GA',CA’,则△CGA'的周长的最小值为__.
【答案】7+![]()
【解析】
如图,当点F固定时,连接AC交EF于G,连接A′G,此时△CGA′的周长最小,最小值=A′G+GC+CA′=GA+GC+CA′=AC+CA′.当CA′最小时,△CGA′的周长最小,求出CA′的最小值即可解决问题.
解:如图,当点F固定时,连接AC交EF于G,连接A′G,此时△A′GC的周长最小,最小值=A′G+GC+CA′=GA+GC+CA′=AC+CA′.

∵四边形ABCD是矩形,
∴∠D=90°,AD=BC=6,CD=AB=8,
∴AC=![]() ,
,
∴△A′CG的周长的最小值=10+CA′,
当CA′最小时,△CGA′的周长最小,
∵AE=DE=EA′=3,
∴CE=![]() ,
,
∵CA′≥EC﹣EA′,
∴CA′≥![]() ﹣3,
﹣3,
∴CA′的最小值为![]() ﹣3,
﹣3,
∴△CGA′的周长的最小值为7+![]() ,
,
故答案为:7+![]() .
.


科目:初中数学 来源: 题型:
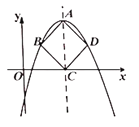
【题目】如图,抛物线![]() (
(![]() )的顶点为
)的顶点为![]() ,对称轴与
,对称轴与![]() 轴交于点
轴交于点![]() ,当以
,当以![]() 为对角线的正方形
为对角线的正方形![]() 的另外两个顶点
的另外两个顶点![]() 、
、![]() 恰好在抛物线上时,我们把这样的抛物线称为美丽抛物线,正方形
恰好在抛物线上时,我们把这样的抛物线称为美丽抛物线,正方形![]() 为它的内接正方形.
为它的内接正方形.
(1)当抛物线![]() 是美丽抛物线时,则
是美丽抛物线时,则![]() ______;当抛物线
______;当抛物线![]() 是美丽抛物线时,则
是美丽抛物线时,则![]() ______;
______;
(2)若抛物线![]() 是美丽抛物线时,则请直接写出
是美丽抛物线时,则请直接写出![]() ,
,![]() 的数量关系;
的数量关系;
(3)若![]() 是美丽抛物线时,(2)
是美丽抛物线时,(2)![]() ,
,![]() 的数量关系成立吗?为什么?
的数量关系成立吗?为什么?
(4)系列美丽抛物线![]() (
(![]() 为小于
为小于![]() 的正整数)顶点在直线
的正整数)顶点在直线![]() 上,且它们中恰有两条美丽抛物线内接正方形面积比为
上,且它们中恰有两条美丽抛物线内接正方形面积比为![]() .求它们二次项系数之和.
.求它们二次项系数之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若干名工人某天生产同一种玩具,生产的玩具数整理成条形图(如图所示).则他们生产的玩具数的平均数、中位数、众数分别为( )

A.5,5,4 B.5,5,5
C.5,4,5 D.5,4,4
查看答案和解析>>
科目:初中数学 来源: 题型:
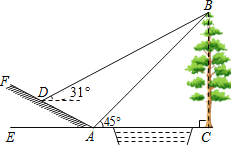
【题目】数学活动课上,小明和小红要测量小河对岸大树BC的高度,小红在点A测得大树顶端B的仰角为45°,小明从A点出发沿斜坡走3![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2.
米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2.
(1)求小明从点A到点D的过程中,他上升的高度;
(2)依据他们测量的数据能否求出大树BC的高度?若能,请计算;若不能,请说明理由.(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在A的正东方向有一港口B.某巡逻艇从A沿着北偏东55°方向巡逻,到达C时接到命令,立刻从C沿南偏东60°方向以20海里/小时的速度航行,从C到B航行了3小时.求A,B间的距离(结果保留整数).(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某运输公司现将一批152吨的货物运往A,B两地,若用大小货车15辆,则恰好能一次性运完这批货.已知这两种大小货车的载货能力分别为12吨/辆和8吨/辆,其运往A,B两地的运费如下表所示:
目的地(车型) | A地(元/辆) | B地(元/辆) |
大货车 | 800 | 900 |
小货车 | 400 | 600 |
(1)求这15辆车中大小货车各多少辆.(用二元一次方程组解答)
(2)现安排其中的10辆货车前往A地,其余货车前往B地,设前往A地的大货车为x辆,前往A,B两地总费用为w元,试求w与x的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】欧几里得在《几何原本》中,记载了用图解法解方程![]() 的方法,类似地可以用折纸的方法求方程
的方法,类似地可以用折纸的方法求方程![]() 的一个正根。下面是甲、乙两位同学的做法:甲:如图1,裁一张边长为1的正方形的纸片
的一个正根。下面是甲、乙两位同学的做法:甲:如图1,裁一张边长为1的正方形的纸片![]() ,先折出
,先折出![]() 的中点
的中点![]() ,再折出线段
,再折出线段![]() ,然后通过折叠使
,然后通过折叠使![]() 落在线段
落在线段![]() 上,折出点
上,折出点![]() 的新位置
的新位置![]() ,因而
,因而![]() ,类似地,在
,类似地,在![]() 上折出点
上折出点![]() 使
使![]() 。此时,
。此时,![]() 的长度可以用来表示方程
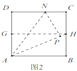
的长度可以用来表示方程![]() 的一个正根;乙:如图2,裁一张边长为1的正方形的纸片
的一个正根;乙:如图2,裁一张边长为1的正方形的纸片![]() ,先折出
,先折出![]() 的中点
的中点![]() ,再折出线段
,再折出线段![]() N,然后通过沿线段
N,然后通过沿线段![]() 折叠使
折叠使![]() 落在线段
落在线段![]() 上,折出点
上,折出点![]() 的新位置
的新位置![]() ,因而
,因而![]() 。此时,
。此时,![]() 的长度可以用来表示方程
的长度可以用来表示方程![]() 的一个正根;甲、乙两人的做法和结果( )。
的一个正根;甲、乙两人的做法和结果( )。

A.甲对,乙错B.乙对,甲错C.甲乙都对D.甲乙都错
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.

(1)求证:四边形ADCF是菱形;
(3)若AC=6,AB=8,求菱形ADCF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com