
【题目】如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆恰好与BC相切于点D,分别交AC,AB于点E,F.
(1)若∠B=30°,求证:以A,O,D,E为顶点的四边形是菱形;
(2)填空:若AC=6,AB=10,连接AD,则⊙O的半径为 ,AD的长为 .

【答案】(1) 见解析;(2)![]()
【解析】
(1) 先通过证明△AOE为等边三角形, 得出AE=OD, 再根据“同位角相等, 两直线平行” 证明AE//OD, 从而证得四边形AODE是平行四边形, 再根据 “一组邻边相等的平行四边形为菱形” 即可得证.
(2) 利用在Rt△OBD中,sin∠B=![]() =
=![]() 可得出半径长度,在Rt△ODB中BD=
可得出半径长度,在Rt△ODB中BD=![]() ,可求得BD的长,由CD=CB﹣BD可得CD的长,在RT△ACD中,AD=
,可求得BD的长,由CD=CB﹣BD可得CD的长,在RT△ACD中,AD=![]() ,即可求出AD长度.
,即可求出AD长度.
解:(1)证明: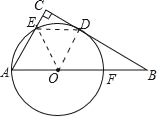
连接OE、ED、OD,
在Rt△ABC中,∵∠B=30°,
∴∠A=60°,
∵OA=OE,∴△AEO是等边三角形,
∴AE=OE=AO
∵OD=OA,
∴AE=OD
∵BC是圆O的切线,OD是半径,
∴∠ODB=90°,又∵∠C=90°
∴AC∥OD,又∵AE=OD
∴四边形AODE是平行四边形,
∵OD=OA
∴四边形AODE是菱形.
(2)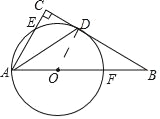
在Rt△ABC中,∵AC=6,AB=10,
∴sin∠B=![]() =
=![]() ,BC=8
,BC=8
∵BC是圆O的切线,OD是半径,
∴∠ODB=90°,
在Rt△OBD中,sin∠B=![]() =
=![]() ,
,
∴OB=![]() OD
OD
∵AO+OB=AB=10,
∴OD+![]() OD=10
OD=10
∴OD=![]()
∴OB=![]() OD=
OD=![]()
∴BD=![]()
=5
∴CD=CB﹣BD=3
∴AD=![]()
=![]()
=3![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1所示的图形,像我们常见的符号——箭号.我们不妨把这样图形叫做“箭头四角形”.
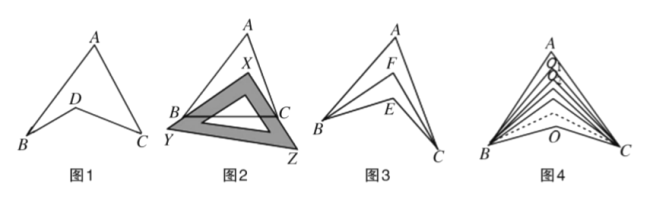
探究:
(1)观察“箭头四角形”,试探究![]() 与
与![]() 、
、![]() 、
、![]() 之间的关系,并说明理由;
之间的关系,并说明理由;
应用:
(2)请你直接利用以上结论,解决以下两个问题:
①如图2,把一块三角尺![]() 放置在
放置在![]() 上,使三角尺的两条直角边
上,使三角尺的两条直角边![]() 、
、![]() 恰好经过点
恰好经过点![]() 、
、![]() ,若
,若![]() ,则
,则![]()
![]() ;
;
②如图3,![]() 、
、![]() 的2等分线(即角平分线)
的2等分线(即角平分线)![]() 、
、![]() 相交于点
相交于点![]() ,若
,若![]() ,
,
![]() ,求
,求![]() 的度数;
的度数;
拓展:
(3)如图4,![]() ,
,![]() 分别是
分别是![]() 、
、![]() 的2020等分线(
的2020等分线(![]() ),它们的交点从上到下依次为
),它们的交点从上到下依次为![]() 、
、![]() 、
、![]() 、…、
、…、![]() .已知
.已知![]() ,
,![]() ,则
,则![]() 度.
度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,B、A、F三点在同一直线上,(1)AD∥BC,(2)∠B=∠C,(3)AD平分∠EAC.
请你用其中两个作为条件,另一个作为结论,构造一个真命题,并证明.
己知:______________________________________________________.
求证:______________________________________________________.
证明:

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明平时喜欢玩“开心消消乐”游戏,本学期在学校组织的几次数学反馈性测试中,小明的数学成绩如下表:
月份 |
|
|
|
|
|
|
成绩(分) |
|
|
|
| ··· | ··· |
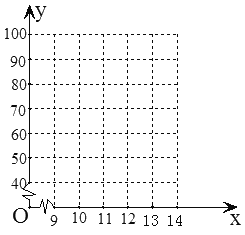
(1)以月份为x轴,成绩为y轴,根据上表提供的数据在平面直角坐标系中描点;
(2)观察(1)中所描点的位置关系,猜想![]() 与
与![]() 之间的的函数关系,并求出所猜想的函数表达式;
之间的的函数关系,并求出所猜想的函数表达式;
(3)若小明继续沉溺于“开心消消乐“游戏,照这样的发展趋势,请你估计元月(此时![]() )份的考试中小明的数学成绩,并用一句话对小明提出一些建议.
)份的考试中小明的数学成绩,并用一句话对小明提出一些建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆恰好与BC相切于点D,分别交AC、AB于点E、F.
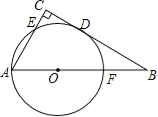
(1)若∠B=30°,求证:以A、O、D、E为顶点的四边形是菱形.
(2)若AC=6,AB=10,连结AD,求⊙O的半径和AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标![]() 中,正比例函数
中,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象经过点
的图象经过点![]() .
.
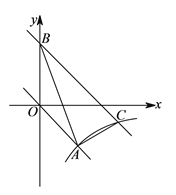
(![]() )分别求这两个函数的表达式.
)分别求这两个函数的表达式.
(![]() )将直线
)将直线![]() 向上平移
向上平移![]() 个单位长度后与
个单位长度后与![]() 轴交于点
轴交于点![]() ,与反比例函数图象在第四象限内的交点为
,与反比例函数图象在第四象限内的交点为![]() ,连接
,连接![]() 、
、![]() ,求点
,求点![]() 的坐标及
的坐标及![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com