
����Ŀ������ѧ��ȤС���У�С��������ѧ̽��������߳�Ϊ2��������ABCD��߳�Ϊ2![]() ��������AEFG��ͼ1λ�÷��ã�AD��AE��ͬһֱ���ϣ�AB��AG��ͬһֱ������
��������AEFG��ͼ1λ�÷��ã�AD��AE��ͬһֱ���ϣ�AB��AG��ͬһֱ������
��1��С������DG��BE���������˵��������
��2����ͼ2��С����������ABCD�Ƶ�A��ʱ����ת������Bǡ�������߶�DG��ʱ��������������ʱBE�ij���
��3����ͼ3��С����������ABCD�Ƶ�A������ʱ����ת���߶�DG���߶�BE���ཻ������ΪH��д����GHE����BHD���֮�͵����ֵ������Ҫ˵��������

���𰸡���1�����ɼ���������2��![]() ����3��6�����ɼ�������
����3��6�����ɼ�������
��������
�����������1�����ı���ABCD���ı���AEFGΪ�����Σ����������ε����ʵõ����Ա���ȣ��Ҽн���ȣ�����SAS�õ�������ADG��������ABEȫ�ȣ�����ȫ�������ζ�Ӧ����ȵ���AGD=��AEB����ͼ1��ʾ���ӳ�EB��DG�ڵ�H�����õȽǵ������ȵõ���DHE=90�������ô�ֱ�Ķ��弴�ɵ�DG��BE��
��2�����ı���ABCD���ı���AEFGΪ�����Σ����������ε����ʵõ����Ա���ȣ��Ҽн���ȣ�����SAS�õ�������ADG��������ABEȫ�ȣ�����ȫ�������ζ�Ӧ����ȵõ�DG=BE����ͼ2������A��AM��DG��DG�ڵ�M����AMD=��AMG=90������ֱ��������AMD�У����AM�ij�����ΪDM�ij������ݹ��ɶ������GM�ij�������ȷ����DG�ij�����ΪBE�ij���
��3����GHE����BHD���֮�͵����ֵΪ6������Ϊ��������EGH����H����EGΪֱ����Բ�ϣ�������H���A�غ�ʱ����EGH�ĸ��������BDH����H����BDΪֱ����Բ�ϣ�������H���A�غ�ʱ����BDH�ĸ������ȷ������������ֵ��
�����������1�����ı���ABCD���ı���AEFG��Ϊ�����Σ�
��AD=AB����DAG=��BAE=90����AG=AE��
����ADG����ABE��
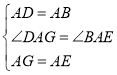 ��
��
���ADG�ա�ABE��SAS����
���AGD=��AEB��
��ͼ1��ʾ���ӳ�EB��DG�ڵ�H��
����ADG����AGD+��ADG=90����
���AEB+��ADG=90����
����EDH����AEB+��ADG+��DHE=180����
���DHE=90����
��DG��BE��
��2�����ı���ABCD���ı���AEFG��Ϊ�����Σ�
��AD=AB����DAB=��GAE=90����AG=AE��
���DAB+��BAG=��GAE+��BAG������DAG=��BAE��
����ADG����ABE��
���ADG�ա�ABE��SAS����
��DG=BE��
��ͼ2������A��AM��DG��DG�ڵ�M����AMD=��AMG=90����
��BDΪ������ABCD�ĶԽ��ߣ�
���MDA=45����
��Rt��AMD����MDA=45����
��cos45��=![]() ��
��
��AD=2��
��DM=AM=![]() ��
��
��Rt��AMG�У����ݹ��ɶ����ã�GM=![]() ��
��
��DG=DM+GM=![]() ��
��
��BE=DG=![]() ��
��
��3����GHE����BHD���֮�͵����ֵΪ6������Ϊ��
������EGH����H����EGΪֱ����Բ�ϣ�
������H���A�غ�ʱ����EGH�ĸ����
������BDH����H����BDΪֱ����Բ�ϣ�
������H���A�غ�ʱ����BDH�ĸ����
����GHE����BHD���֮�͵����ֵΪ2+4=6��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��B����A�������Ϸ���C����A������ƫ��15�㷽������ACB=90�㣬��C����B���ģ� �� 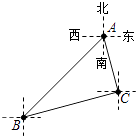
A.��ƫ��75�㷽��
B.��ƫ��65�㷽��
C.��ƫ��60�㷽��
D.��ƫ��30�㷽��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һԪ���η���3x2��4x��1=0�Ķ�����ϵ����һ����ϵ���ֱ�Ϊ�� ��
A.3����1
B.3����4
C.3��4
D.3x2 �� ��4x
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��ʦΪ���˽�ѧ������ѧѧϰ�г�������ľ���������ռ�������ѧ������ҵ�Ϳ����еij�����������10��ѡ���⣬ÿ��3�֣��������̵ij�����1���ࣨ2��������˼�⣮��ͼ��ʾ������������ȡ��10��ѧ���ĵ÷������
��1������ͼ���ṩ����Ϣ����ȫ�±���

��2������24�����ϣ���24�֣���Ϊ�����㡱�������50��ѧ���������������ж�����ѧ���ɼ����㣻
��3���۲�ͼ�����ݷֲ��������ͨ�����㷽��˵���ĸ����ѧ�������ĵ÷�������ȶ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��D���߶�AB���е㣬C���߶�AB�Ĵ�ֱƽ�����ϵ�һ�㣬DE��AC�ڵ�E��DF��BC�ڵ�F��
��1����֤��DE=DF��
��2����CD��AB����������������ϵʱ���ı���CEDFΪ�����Σ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A.4��ƽ������2
B.![]() ��������
��������![]()
C.����������������
D.ʵ���������ϵĵ�һһ��Ӧ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Сѧȫ�濪չ���������������ijУ�ڴ�μ��п�����A����٣�B���ܲ٣�C���赸��D��������������Ϊ�˽�ѧ����ϲ����һ���������ȡ�˲���ѧ�����е��飬�������������Ƴ�������������������ͳ��ͼ�������ͳ��ͼ�ش��������⣺ 
��1����α������ѧ�������ˣ�
��2���뽫ͳ��ͼ2����������
��3��ͳ��ͼ1��B��Ŀ��Ӧ�����ε�Բ�Ľ����ȣ�
��4����֪��У����ѧ��3600�ˣ�����ݵ��������Ƹ�Уϲ�������ٵ�ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�У�AB=AC=10cm��BC=8cm����DΪAB���е㣮 
��1�������P���߶�BC����3cm/s���ٶ���B����C���˶���ͬʱ����Q���߶�CA����C����A���˶���
������Q���˶��ٶ����P���˶��ٶ���ȣ�����1s��BPD���CQP�Ƿ�ȫ�ȣ���˵�����ɣ�
������Q���˶��ٶ����P���˶��ٶȲ���ȣ�����Q���˶��ٶ�Ϊ����ʱ���ܹ�ʹ��BPD���CQPȫ�ȣ�
��2������Q�Ԣ��е��˶��ٶȴӵ�C��������P��ԭ�����˶��ٶȴӵ�Bͬʱ����������ʱ���ء�ABC�����˶������ʱ���P���Q��һ���ڡ�ABC����������������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com