
【题目】如图,D是线段AB的中点,C是线段AB的垂直平分线上的一点,DE⊥AC于点E,DF⊥BC于点F.
(1)求证:DE=DF;
(2)当CD与AB满足怎样的数量关系时,四边形CEDF为正方形?请说明理由.

【答案】(1)证明见解析;(2)四边形CEDF为正方形.理由见解析.
【解析】(1)证明:∵CD垂直平分线AB,∴AC=CB,∴△ABC是等腰三角形.
∵CD⊥AB,∴∠ACD=∠BCD.
∵DE⊥AC,DF⊥BC,∴∠DEC=∠DFC=90°,∴∠EDC=∠FDC.
在△DEC与△DFC中,∵∠ACD=∠BCD,CD=CD,∠EDC=∠FDC,∴△DEC≌△DFC(ASA),∴DE=DF;
(2)解:当AB=2CD时,四边形CEDF为正方形.理由如下:
∵AD=BD,AB=2CD,∴AD=BD=CD,∴∠ACD=45°,∠DCB=45°,∴∠ACB=∠ACD+∠BCD=90°,∴四边形DECF是矩形.
又∵DE=DF,∴四边形CEDF是正方形.



 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】某次考试中,某班级的数学成绩统计图如下.下列说法错误的是( ) 
A.得分在70~80分之间的人数最多
B.该班的总人数为40
C.得分在90~100分之间的人数最少
D.及格(≥60分)人数是26
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学兴趣小组活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2![]() 的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
(1)小明发现DG⊥BE,请你帮他说明理由.
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.
(3)如图3,小明将正方形ABCD绕点A继续逆时针旋转,线段DG与线段BE将相交,交点为H,写出△GHE与△BHD面积之和的最大值,并简要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江苏卫视《最强大脑》曾播出一期“辨脸识人”节目,参赛选手以家庭为单位,每组家庭由爸爸妈妈和宝宝3人组成,爸爸、妈妈和宝宝分散在三块区域,选手需在宝宝中选一个宝宝,然后分别在爸爸区域和妈妈区域中正确找出这个宝宝的父母,不考虑其他因素,仅从数学角度思考,已知在本期比赛中有A、B、C三组家庭进行比赛.
(1)若机器人智能小度选择A组家庭的宝宝,求小度在妈妈区域中正确找出其妈妈的概率;
(2)如果任选一个宝宝(假如选A组家庭),通过列表或树状图的方法,求机器人智能小度至少正确找对宝宝父母其中一人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
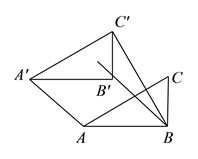
【题目】类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.如图, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,将
,将![]() 沿
沿![]() 的平分线
的平分线![]() 方向平移得到
方向平移得到![]() ,连结
,连结![]() ,
, ![]() .
.
若平移后的四边形![]() 是“等邻边四边形”,求平移的距离(即线段
是“等邻边四边形”,求平移的距离(即线段![]() 的长).
的长).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com