练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．如图，M，N，P，R分别是数轴上四个整数所对应的点，其中有一点是原点，并且MN=NP=PR=1．数a对应的点在M与N之间，数b对应的点在P与R之间，若|a|+|b|=3，则原点是（　　）
    A．M或NB．M或RC．N或PD．P或R

    分析 先利用数轴特点确定a，b的关系从而求出a，b的值，确定原点．

    解答 解：∵MN=NP=PR=1，
    ∴|MN|=|NP|=|PR|=1，
    ∴|MR|=3；
    ①当原点在N或P点时，|a|+|b|＜3，又因为|a|+|b|=3，所以，原点不可能在N或P点；
    ②当原点在M、R时且|Ma|=|bR|时，|a|+|b|=3；
    综上所述，此原点应是在M或R点．
    故选：B．

    点评 此题考查了数轴的定义和绝对值的意义．解此类题的关键是：先利用条件判断出绝对值符号里代数式的正负性，再根据绝对值的性质把绝对值符号去掉，把式子化简后根据整点的特点求解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    12．计算：
    （1）15-[1-（-10-4）]；                  
    （2）-|-32|÷3×（-$\frac{1}{3}$）-（-2）3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．钟表在3点40分时，它的时针和分针所成的角是130度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

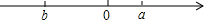    10．对于有理数a，b，定义一种新运算“⊙”，规定a⊙b=|a+b|+|a-b|．
    （1）计算2⊙（-3）的值；
    （2）①当a，b在数轴上的位置如图所示时，化简a⊙b；
    ②当a⊙b=a⊙c时，是否一定有b=c或者b=-c？若是，则说明理由；若不是，则举例说明．
    （3）已知（a⊙a）⊙a=8+a，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

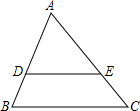    17．如图，△ABC中，DE∥BC，且DE：BC=2：3，则下列结论一定正确的是（　　）
    A．AD：DE=2：3B．AD：BD=2：3C．AD：AE=2：3D．AD：AB=2：3

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．函数y=-2（x-3）2的图象开口向向下，顶点坐标为（3，0），对称轴是过点（3，0）且与y轴平行的直线．其图象可以由函数y=-2x2的图象沿x轴向右平移3个单位长度得到．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

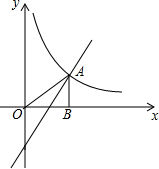    14．一次函数y=kx-1与反比例函数y=$\frac{k}{x}$的图象在第一象限交于点A，过点A作AB⊥x轴于点B，已知S△AOB=1，求反比例函数及一次函数的表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的．下面是一个案例．
    原题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，试说明理由．

    （1）思路梳理
    ∵AB=AD，
    ∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合．
    ∵∠ADC=∠B=90°，
    ∴∠FDG=180°，点F、D、G共线．
    根据SAS，易证△AFG≌△AFE，得EF=BE+DF．  请证明
    类比引申
    如图2，四边形ABCD中，AB=AD，∠BAD=90°点E、F分别在边BC、CD上，∠EAF=45°．若∠B、∠D都不是直角，则当∠B与∠D满足等量关系∠B+∠D=180°时，EF=BE+DF仍然成立，请证明．
    （3）联想拓展
    如图3，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°．猜想BD、DE、EC应满足的等量关系，并写出证明过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．先化简，再求值：（a+b）2+（a-b）（2a-b）-3a2，其中a=$\sqrt{3}$+1，b=$\sqrt{3}$-1．

    查看答案和解析>>

    同步练习册答案