
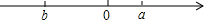 对于有理数a,b,定义一种新运算“⊙”,规定a⊙b=|a+b|+|a-b|.
对于有理数a,b,定义一种新运算“⊙”,规定a⊙b=|a+b|+|a-b|.分析 (1)原式利用题中的新定义计算即可得到结果;
(2)①根据数轴上点的位置判断出a+b与a-b的正负,利用绝对值的代数意义计算即可得到结果;
②当a⊙b=a⊙c时,不一定有b=c或者b=-c,举例即可;
(3)分类讨论a的正负,利用新定义将已知等式化简,即可求出a的值.
解答 解:(1)根据题中的新定义得:2⊙(-3)=|2+(-3)|+|2-(-3)|=1+5=6;
(2)①从a,b在数轴上的位置可得a+b<0,a-b>0,
∴a⊙b=|a+b|+|a-b|=-(a+b)+(a-b)=-2b;
②由a⊙b=a⊙c得:|a+b|+|a-b|=|a+c|+|a-c|,
不一定有b=c或者b=-c,
例如:取a=5,b=4,c=3,则|a+b|+|a-b|=|a+c|+|a-c|=10,
此时等式成立,但b≠c且b≠-c;
(3)当a≥0时,(a⊙a)⊙a=2a⊙a=4a=8+a,
解得:a=$\frac{8}{3}$;
当a<0时,(a⊙a)⊙a=(-2a)⊙a=-4a=8+a,
解得:a=-$\frac{8}{5}$.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,要建一个面积为150㎡的长方形养鸡场,为了节约材料,鸡场的一边靠着原有的一边墙,墙长为18m,另三边用篱笆围成.若篱笆长度为35m,且要求用完.问:
如图,要建一个面积为150㎡的长方形养鸡场,为了节约材料,鸡场的一边靠着原有的一边墙,墙长为18m,另三边用篱笆围成.若篱笆长度为35m,且要求用完.问:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
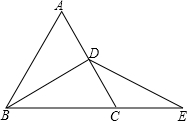 已知:如图,△ABC是等边三角形,BD⊥AC,点E为BC的延长线上一点,BD=DE,
已知:如图,△ABC是等边三角形,BD⊥AC,点E为BC的延长线上一点,BD=DE,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,M,N,P,R分别是数轴上四个整数所对应的点,其中有一点是原点,并且MN=NP=PR=1.数a对应的点在M与N之间,数b对应的点在P与R之间,若|a|+|b|=3,则原点是( )
如图,M,N,P,R分别是数轴上四个整数所对应的点,其中有一点是原点,并且MN=NP=PR=1.数a对应的点在M与N之间,数b对应的点在P与R之间,若|a|+|b|=3,则原点是( )| A. | M或N | B. | M或R | C. | N或P | D. | P或R |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com