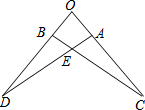
如图.△OAD≌△OBC.且∠O=80°.∠C=20°.则∠AEB=120°．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

19．

如图，△OAD≌△OBC，且∠O=80°，∠C=20°，则∠AEB=120°．

分析根据全等三角形的性质求出∠D，根据三角形外角性质求出∠DBC，再根据三角形的外角性质求出即可．

解答解：∵△OAD≌△OBC，∠C=20°，
∴∠D=∠C=20°，
∵∠O=80°，
∴∠DBC=∠O+∠C=100°，
∴∠AEB=∠D+∠DBC=20°+100°=120°，
故答案为：120．

点评本题考查了三角形的外角性质，全等三角形的性质的应用，能根据全等三角形的性质得出∠D=∠C是解此题的关键，注意：全等三角形的对应角相等，对应边相等．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：填空题

9．如果$\sqrt{2a-1}$有意义，那么a的取值范围是a≥$\frac{1}{2}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

10．

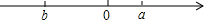对于有理数a，b，定义一种新运算“⊙”，规定a⊙b=|a+b|+|a-b|．
（1）计算2⊙（-3）的值；
（2）①当a，b在数轴上的位置如图所示时，化简a⊙b；
②当a⊙b=a⊙c时，是否一定有b=c或者b=-c？若是，则说明理由；若不是，则举例说明．
（3）已知（a⊙a）⊙a=8+a，求a的值．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

7．函数y=-2（x-3）²的图象开口向向下，顶点坐标为（3，0），对称轴是过点（3，0）且与y轴平行的直线．其图象可以由函数y=-2x²的图象沿x轴向右平移3个单位长度得到．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

14．

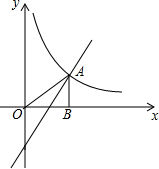一次函数y=kx-1与反比例函数y=$\frac{k}{x}$的图象在第一象限交于点A，过点A作AB⊥x轴于点B，已知S_△AOB=1，求反比例函数及一次函数的表达式．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

4．

如图，A、C两乡镇到水渠边l的距离分别为AB=2km，CD=4km，且BD=8km．
（1）在水渠边l上要建一个水电站P，使得PA+PC最小，请在图中画出P的位置（保留作图痕迹），不必说明理由．
（2）求出PA+PC最小值．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

11．通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的．下面是一个案例．
原题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，试说明理由．

（1）思路梳理
∵AB=AD，
∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合．
∵∠ADC=∠B=90°，
∴∠FDG=180°，点F、D、G共线．
根据SAS，易证△AFG≌△AFE，得EF=BE+DF．请证明
类比引申
如图2，四边形ABCD中，AB=AD，∠BAD=90°点E、F分别在边BC、CD上，∠EAF=45°．若∠B、∠D都不是直角，则当∠B与∠D满足等量关系∠B+∠D=180°时，EF=BE+DF仍然成立，请证明．
（3）联想拓展
如图3，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°．猜想BD、DE、EC应满足的等量关系，并写出证明过程．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

8．

如图所示，⊙O内切于△ABC，若∠ACB=90°，∠AOC=105°，AB=$\frac{8}{3}$，求AC及S_△ABC．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

9．甲、乙两个仓阵要向A、B两地调运小麦．甲可以调出80吨．乙可以调出40吨．A地需要小麦50吨，B需要70吨．
运费如表一：（单位：千米）

	A	B
甲	50	40
乙	80	25

运费如表二：（单位：元/吨千米）

	A	B
甲	2	1
乙	1.5	2

（1）设甲库运往A地x（20≤x≤40）吨求总运费（甲、乙两个仓库的运费之和）y与x之间的函数关系式；
（2）根据（1）中的函数的增减性以及x的取值范围，请确定运费最少的运送方案．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学