
在平面直角坐标系 中,点M(
中,点M( ,
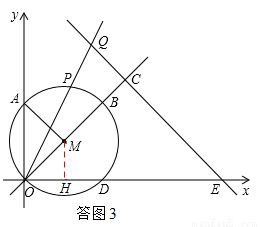
, ),以点M为圆心,OM长为半径作⊙M ,使⊙M与直线OM的另一交点为点B,与
),以点M为圆心,OM长为半径作⊙M ,使⊙M与直线OM的另一交点为点B,与 轴,
轴, 轴的另一交点分别为点D,A(如图),连接AM.点P是
轴的另一交点分别为点D,A(如图),连接AM.点P是 上的动点.
上的动点.
(1)写出∠AMB的度数;
(2)点Q在射线OP上,且OP·OQ=20,过点Q作QC垂直于直线OM,垂足为C,直线QC交 轴于点E.
轴于点E.
①当动点P与点B重合时,求点E的坐标;
②连接QD,设点Q的纵坐标为t,△QOD的面积为S,求S与t的函数关系式及S的取值范围.

(1)90°;(2)①(5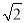 ,0);②S
,0);②S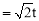 ,5≤S≤10.
,5≤S≤10.
【解析】
试题分析:(1)首先过点M作MH⊥OD于点H,由点M(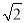 ,
,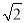 ),可得∠MOH=45°,OH=MH=
),可得∠MOH=45°,OH=MH=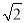 ,继而求得∠AOM=45°,又由OM=AM,可得△AOM是等腰直角三角形,继而可求得∠AMB的度数:
,继而求得∠AOM=45°,又由OM=AM,可得△AOM是等腰直角三角形,继而可求得∠AMB的度数:
如答图3,过点M作MH⊥OD于点H,
∵点M(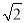 ,
,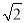 ),∴OH=MH=
),∴OH=MH=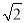 .∴∠MOD=45°.
.∴∠MOD=45°.
∵∠AOD=90°,∴∠AOM=45°.
∵OA=OM,∴∠OAM=∠AOM=45°.∴∠AMO=90°.∴∠AMB=90°.
(2)①由OH=MH=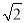 ,MH⊥OD,即可求得OD与OM的值,继而可得OB的长,又由动点P与点B重合时,OP•OQ=20,可求得OQ的长,继而求得答案.
,MH⊥OD,即可求得OD与OM的值,继而可得OB的长,又由动点P与点B重合时,OP•OQ=20,可求得OQ的长,继而求得答案.
②由OD=2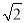 ,Q的纵坐标为t,即可得S=
,Q的纵坐标为t,即可得S=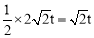 ,然后分别从当动点P与B点重合时,过点Q作QF⊥x轴,垂足为F点,与当动点P与A点重合时,Q点在y轴上,去分析求解即可求得答案.
,然后分别从当动点P与B点重合时,过点Q作QF⊥x轴,垂足为F点,与当动点P与A点重合时,Q点在y轴上,去分析求解即可求得答案.
试题解析:【解析】
(1)90°.
(2)①由题意,易知:OM=2,OD=2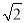 ,∴OB=4.
,∴OB=4.
当动点P与点B重合时,∵OP·OQ=20,∴OQ=5.
∵∠OQE=90°,∠POE=45°,∴OE=5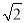 .∴E点坐标为(5
.∴E点坐标为(5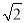 ,0).
,0).
②∵OD=2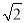 ,Q的纵坐标为t,∴S=
,Q的纵坐标为t,∴S=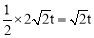 .
.
如答图1,当动点P与B点重合时,过点Q作QF⊥x轴,垂足为F点,
∵OP=4,OP•OQ=20,∴OQ=5,
∵∠OFC=90°,∠QOD=45°,∴t=QF=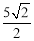 .
.
此时S=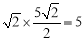 .
.
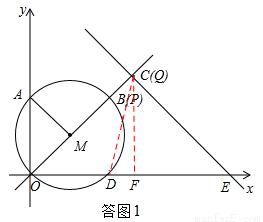
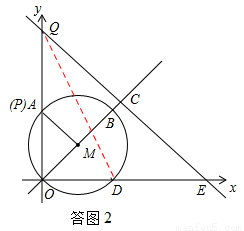
如答图2,当动点P与A点重合时,Q点在y轴上,
∴OP=2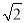 .
.
∵OP•OQ=20,∴t=OQ=5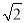 .
.
此时S=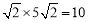 .
.
∴S的取值范围为5≤S≤10.
考点:1.圆的综合题;2.单动点问题;3.等腰直角三角形的判定和性质;4.点的坐标;5.由实际问题列函数关系式;6.数形结合思想、分类思想和方程思想的应用.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源:2014年初中毕业升学考试(江苏淮安卷)数学(解析版) 题型:填空题
一只不透明的袋子中装有1个白球和3个红球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,则摸出红球的概率为 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏徐州卷)数学(解析版) 题型:选择题
将函数y=﹣3x的图象沿y轴向上平移2个单位长度后,所得图象对应的函数关系式为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏常州卷)数学(解析版) 题型:解答题
已知:如图,E,F是四边形ABCD的对角线AC上的两点,AF=CE,连接DE,DF,BE,BF,四边形DEBF为平行四边形.求证:四边形ABCD是平行四边形.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏常州卷)数学(解析版) 题型:填空题
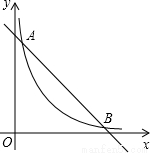
在平面直角坐标系xOy中,一次函数 的图象与函数
的图象与函数 的图象相交于点A,B.设点A的坐标为(x1,y1),那么长为x1,宽为y1的矩形的面积为 ,周长为 .
的图象相交于点A,B.设点A的坐标为(x1,y1),那么长为x1,宽为y1的矩形的面积为 ,周长为 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏宿迁卷)数学(解析版) 题型:解答题
如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com