
 如图,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF.从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….
如图,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF.从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….分析 (1)根据数字排列规律,依次数下去就可以得到)“17”在射线 OE上;
(2)因为正整数按照6个数字一循环,依次排列,因此,出现在每一条射线上的数字都可以看做一个等差数列,根据等差数列通项公式an=a1+(n-1)×d即可写出.
(3)因为正整数按照6个数字一循环,依次排列,所以将2011除以6,如果能被整除,则落在射线OF上,如果有余数,则依次落在OA至OE上.
解答 解:(1)根据已知总结排列如下:
射线OA:1 7 13 19 …
射线OB:2 8 14 20 …
射线OC:3 9 15 21 …
射线OD:4 10 16 22 …
射线OE:5 11 17 23 …
射线OF:6 12 18 24 …
故“17”在射线 OE上.
故答案为:OE.
(2)根据已知总结排列如下:
射线OA:1 7 13 19 …数字排列规律:6n-5 (n为正整数)
射线OB:2 8 14 20 …数字排列规律:6n-4 (n为正整数)
射线OC:3 9 15 21 …数字排列规律:6n-3 (n为正整数)
射线OD:4 10 16 22 …数字排列规律:6n-2 (n为正整数)
射线OE:5 11 17 23 …数字排列规律:6n-1 (n为正整数)
射线OF:6 12 18 24 …数字排列规律:6n (n为正整数)
(3)∵2011÷6=335…1,
根据数字排列6个数字一循环,得2011在射线OA上,
根据射线OB的数字排列规律得:
6n-5=2011,
解得:n=336.
答:“2011”在射线OA的第336个位置.
点评 题目考查了数字的排列规律,考查了学生要从数字的排列中找到规律,然后写出规律即可求出相应值.此外掌握等差数列的通项公式an=a1+(n-1)×d对解决此类问题有很大帮助.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
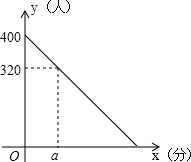 春节期间,某客运站旅客流量不断增大,旅客往往需长时间排队等候购票.经调查发现,每天开始售票时,约有400名旅客排队等候购票,同时又有新的旅客不断进入售票厅排队等候购票.售票时售票厅每分钟新增购票人数4人,每分钟每个售票窗口出售的票数3张,规定每人只购一张票.某天若同时开放两个售票窗口,售票厅排队等候购票的人数y(人)与售票时间x(分)的关系如图所示.
春节期间,某客运站旅客流量不断增大,旅客往往需长时间排队等候购票.经调查发现,每天开始售票时,约有400名旅客排队等候购票,同时又有新的旅客不断进入售票厅排队等候购票.售票时售票厅每分钟新增购票人数4人,每分钟每个售票窗口出售的票数3张,规定每人只购一张票.某天若同时开放两个售票窗口,售票厅排队等候购票的人数y(人)与售票时间x(分)的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
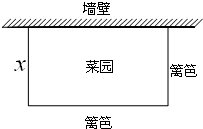 如图,要用长40米的篱笆和一面足够长的废弃墙壁围一个矩形菜园(三面用篱笆,一面用废弃墙壁),若垂直墙壁的一面篱笆长为x,菜园的面积为S.
如图,要用长40米的篱笆和一面足够长的废弃墙壁围一个矩形菜园(三面用篱笆,一面用废弃墙壁),若垂直墙壁的一面篱笆长为x,菜园的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com