
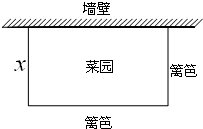
 如图,要用长40米的篱笆和一面足够长的废弃墙壁围一个矩形菜园(三面用篱笆,一面用废弃墙壁),若垂直墙壁的一面篱笆长为x,菜园的面积为S.
如图,要用长40米的篱笆和一面足够长的废弃墙壁围一个矩形菜园(三面用篱笆,一面用废弃墙壁),若垂直墙壁的一面篱笆长为x,菜园的面积为S.分析 (1)先表示出矩形的长,再由矩形的面积公式就可以得出结论;
(2)将(1)的解析式转化为顶点式,由二次函数的性质就可以得出结论.
解答 解:(1)由题意,得
S=x(40-2x),
S=-2x2+40x.
答:S与x之间的函数关系式为S=-2x2+40x;
(2)∵S=-2x2+40x.
∴S=-2(x-10)2+200.
∴a=-2<0,
∴x=10时,y最大=200.
∴长为:40-2×10=20米.
答:这个矩形的长为20米,宽为10米时,菜园的面积最大,最大面积是200平方米.
点评 本题考查了矩形的面积公式的运用,二次函数的解析式的运用,二次函数的顶点式的运用,解答时求出函数的解析式是关键.


科目:初中数学 来源: 题型:选择题
| A. | a≤$\frac{2}{3}$ | B. | a≥$\frac{2}{3}$ | C. | a>$\frac{2}{3}$ | D. | a<$\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF.从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….
如图,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF.从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com