
���� ��1����������֮��ľ�����㷽���Լ���B��λ����ô𰸼��ɣ�
��2�����������ϵ��ƽ�ƹ������ƽ�ƺ����ֵ����һ����������֮��ľ�����ô�ʱA��B�����ľ��뼴�ɣ�
��3�����˶�ʱ��Ϊt�룮
�����������ϵ��ƽ�ƹ�������˶����P��Q����ʾ�������ɣ�
�ڷ�P��Q���Ҳ࣬P��Q����࣬�г����̽�ɣ�
��� �⣺��1�������ϵ�B����ʾ����Ϊ8-12=-4��
��2���յ�B��ʾ������-4+8-4=0����ʱA��B�����ľ��룬8��
��3�����˶�ʱ��Ϊt�룮
�ٵ�P����ʾ����8-at����Q����ʾ����-4+bt��
���������
��P��Q���Ҳ�ʱ����8-at��-��-4+bt��=2����ã�t=$\frac{10}{a+b}$��
P��Q����࣬��-4+bt��-��8-at��=2����ã�t=$\frac{14}{a+b}$��
���˶�$\frac{10}{a+b}$���$\frac{14}{a+b}$��P��Q�������2����λ���ȣ�
���� ���⿼��һԪһ�η��̵�ʵ�����ã���������������֮��ľ����Լ����ƽ�ƹ��ɽ�����⣬ע�����̽������֮��ľ���������֮���λ�ù�ϵ��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
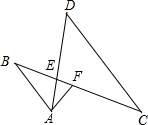 ��֪����ͼ��AB��CD��AD��BC���ڵ�E��FΪBC��һ�㣬�ҡ�EAF=��C��
��֪����ͼ��AB��CD��AD��BC���ڵ�E��FΪBC��һ�㣬�ҡ�EAF=��C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
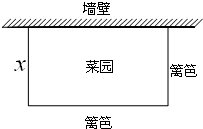 ��ͼ��Ҫ�ó�40����ʺ�һ���㹻���ķ���ǽ��Χһ�����β�����������ʣ�һ���÷���ǽ�ڣ�������ֱǽ�ڵ�һ����ʳ�Ϊx���������ΪS��
��ͼ��Ҫ�ó�40����ʺ�һ���㹻���ķ���ǽ��Χһ�����β�����������ʣ�һ���÷���ǽ�ڣ�������ֱǽ�ڵ�һ����ʳ�Ϊx���������ΪS���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У���A��0��b������B��a��0������D��2��0��������a��b����$\sqrt{a+1}$+|b-3|=0��DE��x�ᣬ�ҡ�BED=��ABO��ֱ��AE��x���ڵ�C��
��ͼ����ƽ��ֱ������ϵ�У���A��0��b������B��a��0������D��2��0��������a��b����$\sqrt{a+1}$+|b-3|=0��DE��x�ᣬ�ҡ�BED=��ABO��ֱ��AE��x���ڵ�C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x+2y=0 | B�� | x2+3x+2=0 | C�� | 2x-3=$\frac{1}{x}$+2 | D�� | x+1=0 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com