
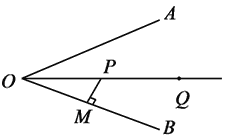
����Ŀ����֪��BOA��һ����·������OPǡ�þ�����Oƽ�֡�AOB��
��1�����Ҫ��P���ƶ�����·��·����̣���ͼ����ʾPM�⣬������ѡ��PN����������·��������·���Ĺ�ϵ��______��������___________��
��2���������δ���һ��Q�����Ҫ��P����������﹫·OA�ϵĵ�C����ǰ����Q�����㻭��һ�����·����������C��λ�ã�
��3��D���ڹ�·OB�ϣ�O�㵽D��ľ�����C����ȣ�������CDP����֤����CDPΪ���������Σ�
���𰸡���1���Գƣ��㵽ֱ�ߵľ��룬���߶���̣���2����ͼ����������3��֤����������
��������
��1������P��OA�Ĵ����ɵã�
��2������P����OA�ĶԳƵ�P��������P��Q����OA�Ľ��㼴Ϊ�����C��
��3������C��OQ�Ĵ��ߣ���OB�ڵ�D�������д��ߺͽ�ƽ���ߵ�����֤�����ɵã�
��1���߶�PNΪ����

��2��P��C��Q·����̣���C��Ϊ����

��3����ͼ����CDP��Ϊ����

������ã�
OC=OD����AOQ=��BOQ��OP=OP��
���COP�ա�DOP��SAS����
��CP=DP��
���CDP����������


 ��һ����ͬ���ɽ�����ϵ�д�
��һ����ͬ���ɽ�����ϵ�д� ������Ӧ���ϵ�д�
������Ӧ���ϵ�д� ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����ACΪֱ������O��BC�ڵ�D������D��EF��AB�ڵ�F����AC���ӳ����ڵ�E�� 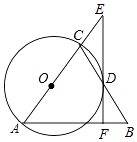
��1���ж�EF���O��λ�ù�ϵ����˵�����ɣ�
��2����AF=6��sinE= ![]() ����BF�ij���
����BF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��D�ǵȱ�������ABC��һ�㣬���߶�AD�Ƶ�A˳ʱ����ת60�㣬�õ��߶�AE������CD��BE��
��1����֤����AEB=��ADC��
��2������DE������ADC=105�㣬����BED�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�AE��BC�ڵ�E�㣬�ӳ�BC��F��ʹCF=BE������AF��DE��DF�� 
��1����֤���ı���AEFD�Ǿ��Σ�
��2����AB=6��DE=8��BF=10����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������1��2��3��4�������г���ͼ��ʾ��һ������
��1����һ�������ڱ��������ס4��������������������Ϊx�����������ú�x��ʽ�ӱ�ʾ�������Ӵ�С�������� ������ ������ ����
��2���ڣ�1����ǰ���£�������ס��4����֮�͵���984ʱ��xλ�ڸñ��ĵڼ��еڼ��У�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ð���Ƥ����ͷ�У�ÿ����Ƥ��������25���������е�40����һ�������������е����һ��ͷ�У�����36�Ű���Ƥ���ö������ƺ������������ƺе���ʹ������е��������ף�
������x���ƺ������ɵ÷���2��25x��40(36��x)��
������x���ƺ������ɵ÷���25x��2��40(36��x)��
������x���ƺ�����y���ƺеף��ɵ÷�����![]() ��
��
������x���ƺ�����y���ƺеף��ɵ÷�����![]() ��������ȷ����( )
��������ȷ����( )
A. �٢� B. �ڢ� C. �ڢ� D. �٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��һ������x1��x2��x3��x4��x5��ƽ������2��������![]() ����ô��һ������3x1��2��3x2��2��3x3��2��3x4��2��3x5��2��ƽ�����ͷ���ֱ��ǣ�������
����ô��һ������3x1��2��3x2��2��3x3��2��3x4��2��3x5��2��ƽ�����ͷ���ֱ��ǣ�������
A. 2��![]() B. 2��1 C. 4��
B. 2��1 C. 4��![]() D. 4��3
D. 4��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һԪ���η���ָ������һ��δ֪������δ֪������ߴ���Ϊ2�ĵ�ʽ����һԪ���η���![]() ��ķ������£���һ�����Ƚ���ʽ��߹���x��������䷽��
��ķ������£���һ�����Ƚ���ʽ��߹���x��������䷽�� ![]() ���ڶ����������ƽ��ʽ�����ڵ�ʽ��ߣ����ಿ���Ƶ���ʽ�ұߣ�
���ڶ����������ƽ��ʽ�����ڵ�ʽ��ߣ����ಿ���Ƶ���ʽ�ұߣ�![]() ��������������ƽ���������㣬���
��������������ƽ���������㣬���![]() ��-3�����IJ������
��-3�����IJ������![]() .���������һԪ���η��̸��ķ�������1����һԪ���η��̣�
.���������һԪ���η��̸��ķ�������1����һԪ���η��̣�![]() ��
��
��2�������ʽ![]() ����Сֵ��
����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��A����2��0����B��0��4������B��Ϊֱ�Ƕ����ڵڶ�����������ֱ�ǡ�ABC��
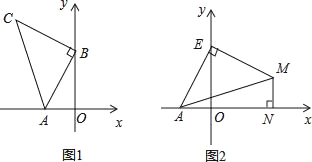
��1����C������ꣻ
��2��������ƽ�����Ƿ����һ��P��ʹ��PAB���ABCȫ�ȣ������ڣ����P�����꣬�������ڣ���˵�����ɣ�
��3����ͼ2����EΪy����������һ���㣬��EΪֱ�Ƕ���������ֱ�ǡ�AEM����M��MN��x����N����OE��MN��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com