
【题目】如图,△ABC中,AC=BC,点D在BC上,作∠ADF=∠B,DF交外角∠ACE的平分线CF于点F. 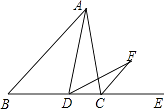
(1)求证:CF∥AB;
(2)若∠CAD=20°,求∠CFD的度数.
【答案】
(1)证明:∵AC=BC,
∴∠B=∠BAC,
∵∠ACE=∠B+∠BAC,
∴∠BAC= ![]() ,
,
∵CF平分∠ACE,
∴∠ACF=∠ECF= ![]() ,
,
∴∠BAC=∠ACF,
∴CF∥AB;
(2)解:∵∠BAC=∠ACF,∠B=∠BAC,∠ADF=∠B,
∴∠ACF=∠ADF,
∵∠ADF+∠CAD+∠AGD=180°,∠ACF+∠F+∠CGF=180°,
又∵∠AGD=∠CGF,
∴∠F=∠CAD=20°
【解析】(1)根据三角形的性质得到∠B=∠BAC,由三角形外角的性质得到∠ACE=∠B+∠BAC,求得∠BAC= ![]() ,由角平分线的定义得到∠ACF=∠ECF=
,由角平分线的定义得到∠ACF=∠ECF= ![]() ,等量代换得到∠BAC=∠ACF,根据平行线的判定定理即可得到结论;(2)由等量代换得到∠ACF=∠ADF,根据三角形的内角和得到∠ADF+∠CAD+∠AGD=180°,∠ACF+∠F+∠CGF=180°,由于∠AGD=∠CGF,即可得到结论.
,等量代换得到∠BAC=∠ACF,根据平行线的判定定理即可得到结论;(2)由等量代换得到∠ACF=∠ADF,根据三角形的内角和得到∠ADF+∠CAD+∠AGD=180°,∠ACF+∠F+∠CGF=180°,由于∠AGD=∠CGF,即可得到结论.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的有( )
①对角线互相平分的四边形是平行四边形;
②平行四边形的对角互补;
③平行线间的线段相等;
④两个全等的三角形可以拼成一个平行四边形;
⑤平行四边形的四内角之比可以是2:3:2:3.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正数范围内定义运算“※”,其规则为a※b=a+b2 , 则方程x※(x+1)=5的解是( )
A.x=5
B.x=1
C.x1=1,x2=﹣4
D.x1=﹣1,x2=4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个饲养场里的鸡的只数与猪的头数之和是70,鸡、猪的腿数之和是196,设鸡的只数是x , 依题意列方程为( )
A.2x+4(70-x)=196
B.2x+4×70=196
C.4x+2(70-x)=196
D.4x+2×70=196
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生环保意识,某中学组织全校2000名学生参加环保知识大赛,比赛成绩均为整数,从中抽取部分同学的成绩进行统计,并绘制成如图统计图.请根据图中提供的信息,解答下列问题:
(1)若抽取的成绩用扇形图来描述,则表示“第三组(79.5~89.5)”的扇形的圆心角为 度;
(2)若成绩在90分以上(含90分)的同学可以获奖,请估计该校约有多少名同学获奖?
(3)某班准备从成绩最好的4名同学(男、女各2名)中随机选取2名同学去社区进行环保宣传,则选出的同学恰好是1男1女的概率为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛预赛.各参赛选手的成绩如图:
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:

(1)直接写出表中m、n的值;
(2)依据数据分析表,有人说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有人说(2)班的成绩要好,请给出两条支持九(2)班成绩好的理由;
(3)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,试求另外两个决赛名额落在同一个班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点P(﹣2,3)与点Q关于原点对称,则点Q的坐标为( )
A.(﹣2,﹣3)
B.(3,﹣2)
C.(2,3)
D.(2,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( ) 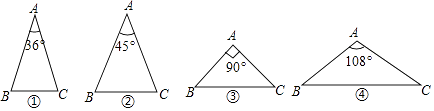
A.①③
B.①②④
C.①③④
D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com