
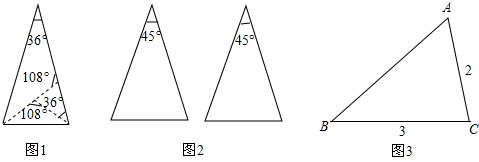
分析 (1)根据等腰三角形的判定定理容易画出图形;由等腰三角形的性质即可求出各个顶角的度数;
(2)根据等腰三角形的判定定理容易画出图形;设∠B=α,则∠DCB=∠DCA=∠EAC=α,∠ADE=∠AED=2α,则△AEC∽△BDC,△ACD∽△ABC,得出对应边成比例,设AE=AD=x,BD=CD=y,得出方程组,解方程组即可.
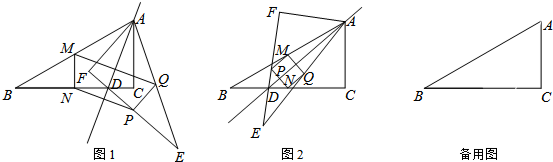
解答 解:(1)作图如图1、图2所示: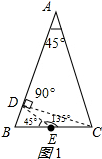
在图1中,
∵AD=CD,
∴∠ACD=∠A=45°,
∴∠ADC=90°;
∵AB=AC,∠A=45°,
∴∠B=∠ACB=67.5°,
∴∠ECD=67.5°-45°=22.5°,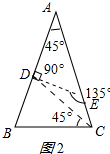
∵DE=CE,
∴∠EDC=∠ECD=22.5°,
∴∠DEC=135°,
∴∠BED=45°,
即三个等腰三角形的顶角分别为90°、135°、45°;
在图2中,∵AD=DE,
∴∠DEA=∠A=45°,
∴∠ADE=90°,∠DEC=135°;
∵BC=DC,
∴∠CDB=∠B=67.5°,
∴∠BCD=45°,
即三个等腰三角形的顶角分别为90°、135°、45°;
(2)如图3所示,CD、AE就是所求的三分线.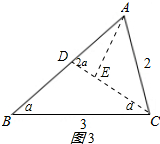
设∠B=α,则∠DCB=∠DCA=∠EAC=α,∠ADE=∠AED=2α,
此时△AEC∽△BDC,△ACD∽△ABC,
设AE=AD=x,BD=CD=y,
∵△AEC∽△BDC,
∴x:y=2:3,
∵△ACD∽△ABC,
∴2:x=(x+y):2,
解方程组$\left\{\begin{array}{l}{x:y=2:3}\\{2:x=(x+y):2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{2\sqrt{10}}{5}}\\{y=\frac{3\sqrt{10}}{5}}\end{array}\right.$,或$\left\{\begin{array}{l}{x=-\frac{2\sqrt{10}}{5}}\\{y=-\frac{3\sqrt{10}}{5}}\end{array}\right.$ (负值舍去),
∴AE=$\frac{2\sqrt{10}}{5}$,CD=$\frac{3\sqrt{10}}{5}$,
即三分线长分别是$\frac{3\sqrt{10}}{5}$ 和$\frac{2\sqrt{10}}{5}$.
点评 本题是相似形综合题目,考查了等腰三角形的判定与性质、等腰三角形的画图、相似三角形的判定与性质、解方程组等知识;本题综合性强,有一定难度.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
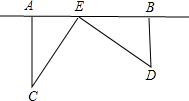 为了丰富少年儿童的业余生活,某社区要在如图中的AB所在的直线上建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B.已知AB=2.5km,CA=1.5km,DB=1.0km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?
为了丰富少年儿童的业余生活,某社区要在如图中的AB所在的直线上建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B.已知AB=2.5km,CA=1.5km,DB=1.0km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
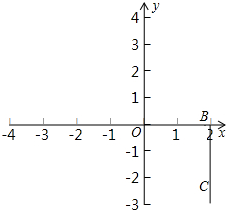 如图,长方形ABCD三个顶点的坐标分别是A(0,0),B(2,0),C(2,-2).
如图,长方形ABCD三个顶点的坐标分别是A(0,0),B(2,0),C(2,-2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
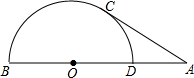 如图,点D为定线段AB上一动点,以BD为直径作半圆O,过A作半圆O的切线,切点为C,连CD,当(AC-AD)取最大值时,tan∠ACD=( )
如图,点D为定线段AB上一动点,以BD为直径作半圆O,过A作半圆O的切线,切点为C,连CD,当(AC-AD)取最大值时,tan∠ACD=( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com