
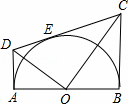
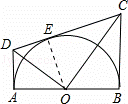
如图,AB为半圆O的在直径,AD、BC分别切⊙O于A、B两点,CD切⊙O于 点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2,④OD:OC=DE:EC,⑤OD2=DE•CD,正确的有( )
点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2,④OD:OC=DE:EC,⑤OD2=DE•CD,正确的有( )
|
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
D解:连接OE,如图所示:
∵AD与圆O相切,DC与圆O相切,BC与圆O相切,
∴∠DAO=∠DEO=∠OBC=90°,
∴DA=DE,CE=CB,AD∥BC,
∴CD=DE+EC=AD+BC,选项②正确;
在Rt△ADO和Rt△EDO中,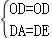 ,
,
∴Rt△ADO≌Rt△EDO(HL),
∴∠AOD=∠EOD,
同理Rt△CEO≌Rt△CBO,
∴∠EOC=∠BOC,
又∠AOD+∠DOE+∠EOC+∠COB=180°,
∴2(∠DOE+∠EOC)=180°,即∠DOC=90°,选项⑤正确;
∴∠DOC=∠DEO=90°,又∠ED O=∠ODC,
O=∠ODC,
∴△EDO∽△ODC,
∴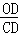 =
=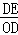 ,即OD2=DC•DE,选项①正确;
,即OD2=DC•DE,选项①正确;
∵∠AOD+∠COB=∠AOD+∠ADO=90°,
∠A=∠B=90°,
∴△AOD∽△BOC,
∴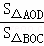 =
=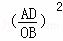 =
=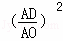 =
=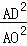 ,选项③正确;
,选项③正确;
同理△ODE∽△OEC,
∴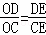 ,选项④正确;
,选项④正确;
故选D.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
如图,已知△ABC的三边长为 、
、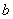 、
、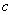 ,且
,且 ,若平行于三角形一边的直线
,若平行于三角形一边的直线
将 △ABC的周长分成相等的两部分,设图中的小三角形①、②、③的面积分别为
△ABC的周长分成相等的两部分,设图中的小三角形①、②、③的面积分别为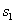 、
、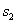 、
、
 则
则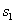 、
、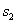 、
、 的大小关系是 (用“<”号连接)
的大小关系是 (用“<”号连接)

查看答案和解析>>
科目:初中数学 来源: 题型:
李明准备进行如下操作实验,把一根长40cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.
(1)要使这两个正方形的面积之和等于58cm2,李明应该怎么剪这根铁丝?
(2)李明认为这两个正方形的面积之和不可能等于48cm2,你认为他的说法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
下列命题正确的是( )
|
| A. | 矩形的对角线互相垂直 |
|
| B. | 两边和一角对应相等的两个三角形全等 |
|
| C. | 分式方程 |
|
| D. | 多项式t2﹣16+3t因式分解为(t+4)(t﹣4)+3t |
查看答案和解析>>
科目:初中数学 来源: 题型:
对于任意实数m、n,定义一种运运算m※n=mn﹣m﹣n+3,等式的右边是通常的加减和乘法运算,例如:3※5=3×5﹣3﹣5+3=10.请根据上述定义解决问题:若a<2※x<7,且解集中有两个整数解,则a的取值范围是
查看答案和解析>>
科目:初中数学 来源: 题型:
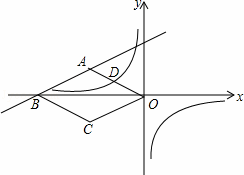
如图,在平面直角坐标系中,四边形ABCD是菱形,B、O在x轴负半轴上,AO=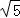 ,tan∠AOB=
,tan∠AOB=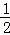 ,一次函数y=k1x+b的图象过A、B两点,反比例函数y=
,一次函数y=k1x+b的图象过A、B两点,反比例函数y= 的图象过OA的中点D.
的图象过OA的中点D.
(1)求一次函数和反比例函数的表达式;
(2)平移一次函数y=k1x+b的图象,当一次函数y=k1x+b的图象与反比例函数y=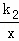 的图象无交点时,求b的取值范围.
的图象无交点时,求b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com