
����Ŀ����1�����ⷢ��
��ͼ1����ACB�͡�DCE��Ϊ�ȱ������Σ���A��D��E��ͬһֱ���ϣ�����BE��
��գ�
�١�AEB�Ķ���Ϊ___________��
���߶�AD��BE֮���������ϵΪ___________��
��2����չ̽��
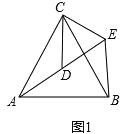
��ͼ2����ACB�͡�DCE��Ϊ����ֱ�������Σ���ACB=��DCE=90�㣬��A��D��E��ͬһֱ���ϣ�CMΪ��DCE��DE���ϵĸߣ�����BE�����жϡ�AEB�Ķ������߶�CM��AE��BE֮���������ϵ����˵�����ɣ�
��3���������
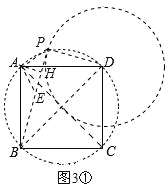
��ͼ3����������ABCD�У�CD=![]() ������P����PD=1���ҡ�BPD=90�㣬��ֱ��д����A��BP�ľ��룮
������P����PD=1���ҡ�BPD=90�㣬��ֱ��д����A��BP�ľ��룮

���𰸡���1����60������AD=BE����2����AEB=90�㣬AE=BE+2CM�����ɼ���������3��![]() ��
��![]() ��
��
��������
�����������1������ͼ1���ߡ�ACB�͡�DCE��Ϊ�ȱ������Σ���CA=CB��CD=CE����ACB=��DCE=60�㣮���ACD=��BCE���ڡ�ACD�͡�BCE�У�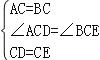 �����ACD�ա�BCE��SAS�������ADC=��BEC���ߡ�DCEΪ�ȱ������Σ����CDE=��CED=60�㣮�ߵ�A��D��E��ͬһֱ���ϣ����ADC=120�㣮���BEC=120�㣮���AEB=��BEC����CED=60�㣮�ʴ�Ϊ��60�㣮
�����ACD�ա�BCE��SAS�������ADC=��BEC���ߡ�DCEΪ�ȱ������Σ����CDE=��CED=60�㣮�ߵ�A��D��E��ͬһֱ���ϣ����ADC=120�㣮���BEC=120�㣮���AEB=��BEC����CED=60�㣮�ʴ�Ϊ��60�㣮
�ڡߡ�ACD�ա�BCE����AD=BE���ʴ�Ϊ��AD=BE��
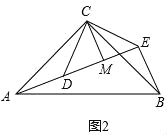
��2����AEB=90�㣬AE=BE+2CM�����ɣ���ͼ2���ߡ�ACB�͡�DCE��Ϊ����ֱ�������Σ���CA=CB��CD=CE����ACB=��DCE=90�㣮���ACD=��BCE���ڡ�ACD�͡�BCE�У�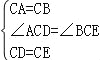 �����ACD�ա�BCE��SAS������AD=BE����ADC=��BEC���ߡ�DCEΪ����ֱ�������Σ����CDE=��CED=45�㣮�ߵ�A��D��E��ͬһֱ���ϣ����ADC=135�㣮���BEC=135�㣮���AEB=��BEC����CED=90�㣮��CD=CE��CM��DE����DM=ME���ߡ�DCE=90�㣬��DM=ME=CM����AE=AD+DE=BE+2CM��
�����ACD�ա�BCE��SAS������AD=BE����ADC=��BEC���ߡ�DCEΪ����ֱ�������Σ����CDE=��CED=45�㣮�ߵ�A��D��E��ͬһֱ���ϣ����ADC=135�㣮���BEC=135�㣮���AEB=��BEC����CED=90�㣮��CD=CE��CM��DE����DM=ME���ߡ�DCE=90�㣬��DM=ME=CM����AE=AD+DE=BE+2CM��
��3����A��BP�ľ���Ϊ![]() ��
��![]() ���������£���PD=1�����P���Ե�DΪԲ�ģ�1Ϊ�뾶��Բ�ϣ��ߡ�BPD=90�㣬���P����BDΪֱ����Բ�ϣ����P������Բ�Ľ��㣮
���������£���PD=1�����P���Ե�DΪԲ�ģ�1Ϊ�뾶��Բ�ϣ��ߡ�BPD=90�㣬���P����BDΪֱ����Բ�ϣ����P������Բ�Ľ��㣮
�ٵ���P����ͼ3����ʾλ��ʱ������PD��PB��PA����AH��BP������ΪH������A��AE��AP����BP�ڵ�E����ͼ3�٣����ı���ABCD�������Σ����ADB=45�㣮AB=AD=DC=BC=![]() ����BAD=90�㣮��BD=2����DP=1����BP=
����BAD=90�㣮��BD=2����DP=1����BP=![]() ���ߡ�BPD=��BAD=90�㣬��A��P��D��B����BDΪֱ����Բ�ϣ����APB=��ADB=45�㣮���PAE�ǵ���ֱ�������Σ��֡ߡ�BAD�ǵ���ֱ�������Σ���B��E��P���ߣ�AH��BP�����ɣ�2���еĽ��ۿɵã�BP=2AH+PD����
���ߡ�BPD=��BAD=90�㣬��A��P��D��B����BDΪֱ����Բ�ϣ����APB=��ADB=45�㣮���PAE�ǵ���ֱ�������Σ��֡ߡ�BAD�ǵ���ֱ�������Σ���B��E��P���ߣ�AH��BP�����ɣ�2���еĽ��ۿɵã�BP=2AH+PD����![]() =2AH+1����AH=
=2AH+1����AH=![]() ��
��
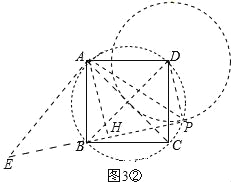
�ڵ���P����ͼ3����ʾλ��ʱ������PD��PB��PA����AH��BP������ΪH������A��AE��AP����PB���ӳ����ڵ�E����ͼ3�ڣ�ͬ���ɵã�BP=2AH��PD����![]() =2AH��1����AH=
=2AH��1����AH=![]() ��������������A��BP�ľ���Ϊ
��������������A��BP�ľ���Ϊ![]() ��
��![]() ��
��


 Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y��3x2����ƽ��������λ��������ƽ��4����λ�������������ǣ� ��
A. y��3��x��2��2��4 B. y��3��x��2��2��4
C. y��3��x��2��2��4 D. y��3��x��2��2��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڳ�Ϊ10����Ϊ8�ľ���ABCD�У���E�ڳ�AD�ϣ�F��BC�ϣ������õ��ľ���EFCD����ABCD������AE֮���Ƕ��٣���˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD�������ϵ�λ����ͼ��ʾ����D��A��Ӧ�����ֱ�Ϊ0��1����������ABCD���Ŷ���˳ʱ�뷽����������������ת����ת1�κ�B����Ӧ����Ϊ2����ת2016�κ���������2016����Ӧ�ĵ��ǣ�������

A. ��C B. ��D C. ��A D. ��B
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Բ�������������µ�ͶӰ�������ǣ�������
A. Բ�� B. �߶� C. ���� D. ��Բ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У���ABC=90�㣬AC=AD��M��N�ֱ�ΪAC��AD���е㣬
�ҡ�ABM=��BAM������BM��MN��BN��
��1����֤��BM=MN��
��2����BAD=60�㣬ACƽ�֡�BAD��AC=2����BN�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ϱ�ʾ��Ϊ�෴����������֮��ľ���Ϊ10�������������ʾ����Ϊ( )
A. 10 B. ��10 C. 5 D. ��5
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com