
【题目】在![]() 中,
中,![]() ,现将
,现将![]() 折叠,使点
折叠,使点![]() 、
、![]() 两点重合,折痕所在的直线与直线
两点重合,折痕所在的直线与直线![]() 的夹角为
的夹角为![]() ,则
,则![]() 的大小为__________度.
的大小为__________度.
【答案】![]() 或
或![]()
【解析】
首先根据题意画出图形,如图1,如图1:由翻折的性质可知:EF⊥AB,所以∠A+∠AFE=90°,从而可求得∠A=40°,然后根据等腰三角形的性质和三角形的内角和定理可求得∠B=70°;如图2;由翻折的性质可知:EF⊥AB,∠D+∠DAE=90°,故此∠DAE=40°,然后由等腰三角形的性质和三角形的外角的性质可求得∠B=20°.
如图1:
由翻折的性质可知:EF⊥AB,
∴∠A+∠AFE=90°.
∴∠A=90°-50°=40°,
∵AB=AC,
∴∠B=∠C.
∴∠B=![]() ×(180°-∠A)=
×(180°-∠A)=![]() ×(180°40°)=70°;
×(180°40°)=70°;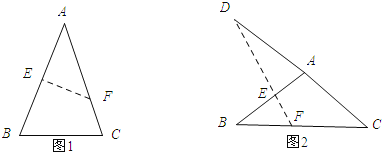
如图2;由翻折的性质可知:EF⊥AB,
∴∠D+∠DAE=90°.
∴∠DAE=90°-50°=40°,
∵AB=AC,
∴∠B=∠C.
∵∠B+∠C=∠DAE,
∴∠B=![]() ∠DAE=
∠DAE=![]() ×40°=20°.
×40°=20°.
故答案为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】苏科版《数学》八年级上册第35页第2题,介绍了应用构造全等三角形的方法测量了池塘两端A、B两点的距离.星期天,爱动脑筋的小刚同学用下面的方法也能够测量出家门前池塘两端A、B两点的距离.他是这样做的:
选定一个点P,连接PA、PB,在PM上取一点C,恰好有PA=14m,PB=13m,PC=5m,BC=12m,他立即确定池塘两端A、B两点的距离为15m.
小刚同学测量的结果正确吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC是边长为3cm等边三角形,动点P、Q分别同时从A、B两点出发,分别沿AB、BC方向匀速移动,点P速度为1cm/s,点Q的速度为2cm/s,当点Q到达点C时,P、Q两点停止运动,设点P的运动时间为t(s),
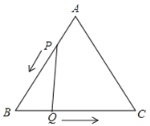
⑴当t为何值时,△PBQ是直角三角形?
⑵△PBQ能否成为等边三角形?若能,请求出t值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“等角三角形”.从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.

(1)如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,请写出图中两对“等角三角形”.
(2)如图2,在△ABC中,CD为角平分线,∠A=40°,∠B=60°。求证:CD为△ABC的等角分割线.
(3)在△ABC中,∠A=42°,CD是△ABC的等角分割线,若△ACD是等腰三角形,请直接写出∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两个港口,水由A流向B,水流的速度是4千米/小时,甲、乙两船同时由A顺流驶向B,各自不停地在A、B之间往返航行,甲在静水中的速度是28千米/小时,乙在静水中的速度是20千米/小时.

设甲行驶的时间为t小时,甲船距B港口的距离为S1千米,乙船距B港口的距离为S2千米,如图为S1(千米)和t(小时)函数关系的部分图象.
(1)A、B两港口距离是_____千米.
(2)在图中画出乙船从出发到第一次返回A港口这段时间内,S2(千米)和t(小时)的函数关系的图象.
(3)求甲、乙两船第二次(不算开始时甲、乙在A处的那一次)相遇点M位于A、B港口的什么位置?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一条笔直公路BD的正上方A处有一探测仪,AD=24m,∠D=90°,一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°.
(Ⅰ)求B,C两点间的距离(结果精确到1m);
(Ⅱ)若规定该路段的速度不得超过15m/s,判断此轿车是否超速.
参考数据:tan31°≈0.6,tan50°≈1.2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形BEFG的边BG在正方形ABCD的边BC上,连结AG,EC.
(1)说出AG与CE的大小关系;
(2)图中是否存在通过旋转能够相互重合的两个三角形?若存在,请详细写出旋转过程;若不存在,请说明理由.
(3)请你延长AG交CE于点M,判断AM与CE的位置关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y=2x与反比例函数y=![]() (k>0)的图象交于A、B两点,且点A的横坐标为4,
(k>0)的图象交于A、B两点,且点A的横坐标为4,
(1)求k的值;
(2)根据图象直接写出正比例函数值小于反比例函数值时x的取值范围;
(3)过原点O的另一条直线l交双曲线y=![]() (k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为224,求点P的坐标.
(k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为224,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com