【题目】如图，点P是∠AOB内任意一点，OP＝5，M，N分别是射线OA和OB上的动点，若△PMN周长的最小值为5，则∠AOB的度数为_____．
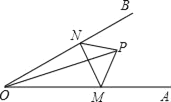
【答案】30°．
【解析】
如图：分别作点P关于OB、AO的对称点P'、P'，分别连OP'、O P'、P' P'交OB、OA于M、N，则可证明此时△PMN周长的最小，由轴对称性，可证明△P'O P'为等边三角形，∠AOB=
∠P'O P'=30°.
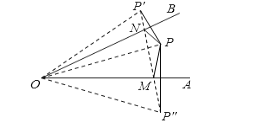
解：如图：分别作点P关于OB、AO的对称点P'、P'，分别连OP'、O 、P' 交OB、OA于M、N，
由轴对称△PMN周长等于PN+NM+MP=P'N+NM+MP"=P'P"
∴由两点之间线段最短可知，此时△PMN周长的最小
∴P'P"=5
由对称OP=OP'=OP"=5
∴△P'OP"为等边三角形
∴∠P'OP"=60
∵∠P'OB=∠POB，∠P"OA=∠POA
∴∠AOB= ∠P'O P'=30°.
故答案为：30°.
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，点A(n，0)是 x 轴上一点，点 B(0，m)是y轴上一点，且满足多项式(x＋m)(nx－2)的积中 x的二次项与一次项系数均为2.
（1）求出A,B两点坐标.
（2）如图1，点M为线段OA上一点，点P为 x 轴上一点，且满足BM＝MN，∠NAP=45°，证明：BM⊥MN.
（3）如图2，过O作OF⊥AB于F，以OB为边在y轴左侧作等边△OBM，连接AM交OF于点N，试探究：在线段AF，AN，MN中，哪条线段等于AM与ON差的一半？请写出这个等量关系并证明.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，如图，等腰△ABC，AB＝AC，∠BAC＝120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP＝OC，下列结论：①AC平分∠PAD；②∠APO＝∠DCO；③△OPC是等边三角形；④AC＝AO+AP；其中正确的序号是（ ）
A.①③④B.②③C.①②④D.①③
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，已知点D，E，F分别为BC，AD，AE的中点，且S△ABC=4cm2，则阴影部分面积S=（ ）cm2．
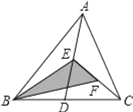
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB∥CD，∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H，∠K﹣∠H=27°，则∠K=（ ）
A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，△ABC中，AB=AC=6，∠A=45°，点D在AC上，点E在BD上，且△ABD、△CDE、△BCE均为等腰三角形．
（1）求∠EBC的度数；
（2）求BE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知RtΔABC,∠C=90°，D为BC的中点.以AC为直径的圆O交AB于点E.
（1）求证：DE是圆O的切线.
(2)若AE:EB=1:2,BC=6，求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
