
【题目】已知:如图,△ABC中,AB=AC=6,∠A=45°,点D在AC上,点E在BD上,且△ABD、△CDE、△BCE均为等腰三角形.

(1)求∠EBC的度数;
(2)求BE的长.
【答案】(1)22.5°;(2)6![]() ﹣6.
﹣6.
【解析】
试题(1)由AB=AC=6,∠A=45°,可求得∠ABC的度数,又由AD=BD,可求得∠ABD的度数,继而求得答案;
(2)由AB=AC=6,∠A=45°,可求得BD的长,然后设DE=EC=x,可得BE=EC=![]() x,即可得方程
x,即可得方程![]() x+x=3
x+x=3![]() ,继而求得答案.
,继而求得答案.
解:(1)∵AB=AC=6,∠A=45°,
∴∠ABC=∠ACB=67.5°,
∵△ABD是等腰三角形,AD=BD,
∴∠ABD=∠A=45°,
∴∠EBC=∠ABC﹣∠ABD=22.5°;
(2)∵∠A=∠ABD=45°,
∴∠ADB=∠CDE=90°,
∵AB=6,
∴BD=ABcos45°=3![]() ,
,
设DE=x,则CD=DE=x,
∴EC=![]() =
=![]() x,
x,
∵BE=EC=![]() x,
x,
∴![]() x+x=3
x+x=3![]() ,
,
解得:x=6﹣3![]() ,
,
∴BE=6![]() ﹣6.
﹣6.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程mx2+(1﹣5m)x﹣5=0(m≠0).
(1)求证:无论m为任何非零实数,此方程总有两个实数根;
(2)若抛物线y=mx2+(1﹣5m)x﹣5与x轴交于A(x1,0)、B(x2,0)两点,且|x1﹣x2|=6,求m的值;
(3)若m>0,点P(a,b)与Q(a+n,b)在(2)中的抛物线上(点P、Q不重合),求代数式4a2﹣n2+8n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织一项公益知识竞赛,比赛规定:每个班级由2名男生、2名女生及1名班主任老师组成代表队.但参赛时,每班只能有3名队员上场参赛,班主任老师必须参加,另外2名队员分别在2名男生和2名女生中各随机抽出1名.初三(1)班由甲、乙2名男生和丙、丁2名女生及1名班主任组成了代表队,求恰好抽到由男生甲、女生丙和这位班主任一起上场参赛的概率.(请用“画树状图”或“列表”或“列举”等方法给出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A1,A2,A3和B1,B2,B3分别在直线y=![]() 和x轴上,△OA1B1,△B1A2B2,△B2A3B3都是等腰直角三角形.则A3的坐标为_______.
和x轴上,△OA1B1,△B1A2B2,△B2A3B3都是等腰直角三角形.则A3的坐标为_______.
 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC是边长为3cm等边三角形,动点P、Q分别同时从A、B两点出发,分别沿AB、BC方向匀速移动,点P速度为1cm/s,点Q的速度为2cm/s,当点Q到达点C时,P、Q两点停止运动,设点P的运动时间为t(s),
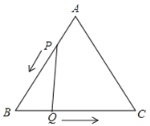
⑴当t为何值时,△PBQ是直角三角形?
⑵△PBQ能否成为等边三角形?若能,请求出t值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“等角三角形”.从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.

(1)如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,请写出图中两对“等角三角形”.
(2)如图2,在△ABC中,CD为角平分线,∠A=40°,∠B=60°。求证:CD为△ABC的等角分割线.
(3)在△ABC中,∠A=42°,CD是△ABC的等角分割线,若△ACD是等腰三角形,请直接写出∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一条笔直公路BD的正上方A处有一探测仪,AD=24m,∠D=90°,一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°.
(Ⅰ)求B,C两点间的距离(结果精确到1m);
(Ⅱ)若规定该路段的速度不得超过15m/s,判断此轿车是否超速.
参考数据:tan31°≈0.6,tan50°≈1.2.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com