
【题目】已知,如图,等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下列结论:①AC平分∠PAD;②∠APO=∠DCO;③△OPC是等边三角形;④AC=AO+AP;其中正确的序号是( )

A.①③④B.②③C.①②④D.①③
【答案】A
【解析】
①利用等腰三角形等边对等角和三角形外角的性质得到∠PAC=∠DAC=60°,从而判断;
②因为点O是线段AD上一点,所以BO不一定是∠ABD的角平分线,可作判断;
③证明∠POC=60°且OP=OC,即可证得△OPC是等边三角形;
④首先证明△OPA≌△CPE,则AO=CE,AC=AE+CE=AO+AP.
解:①∵AB=AC,∠BAC=120°,AD⊥BC;
∴∠CAD=![]() ∠BAC=60°,∠PAC=180°﹣∠CAB=60°,
∠BAC=60°,∠PAC=180°﹣∠CAB=60°,
∴∠PAC=∠DAC,
∴AC平分∠PAD,故①正确;
②由①知:∠APO=∠ABO,∠DCO=∠DBO,
∵点O是线段AD上一点,
∴∠ABO与∠DBO不一定相等,则∠APO与∠DCO不一定相等,
故②不正确;
③∵∠APC+∠DCP+∠PBC=180°,
∴∠APC+∠DCP=150°,
∵∠APO+∠DCO=30°,
∴∠OPC+∠OCP=120°,
∴∠POC=180°﹣(∠OPC+∠OCP)=60°,
∵OP=OC,
∴△OPC是等边三角形;
故③正确;
④如图,在AC上截取AE=PA,
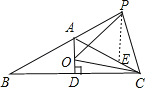
∵∠PAE=180°﹣∠BAC=60°,
∴△APE是等边三角形,
∴∠PEA=∠APE=60°,PE=PA,
∴∠APO+∠OPE=60°,
∵∠OPE+∠CPE=∠CPO=60°,
∴∠APO=∠CPE,
∵OP=CP,
在△OPA和△CPE中, ,
,
∴△OPA≌△CPE(SAS),
∴AO=CE,
∴AC=AE+CE=AO+AP;
故④正确.
故选:A.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,点D、E分别是AB、AC上一点,且AD=AE,∠ABE=∠ACD,BE与CD相交于点F.试判断△BCF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程mx2+(1﹣5m)x﹣5=0(m≠0).
(1)求证:无论m为任何非零实数,此方程总有两个实数根;
(2)若抛物线y=mx2+(1﹣5m)x﹣5与x轴交于A(x1,0)、B(x2,0)两点,且|x1﹣x2|=6,求m的值;
(3)若m>0,点P(a,b)与Q(a+n,b)在(2)中的抛物线上(点P、Q不重合),求代数式4a2﹣n2+8n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】苏科版《数学》八年级上册第35页第2题,介绍了应用构造全等三角形的方法测量了池塘两端A、B两点的距离.星期天,爱动脑筋的小刚同学用下面的方法也能够测量出家门前池塘两端A、B两点的距离.他是这样做的:
选定一个点P,连接PA、PB,在PM上取一点C,恰好有PA=14m,PB=13m,PC=5m,BC=12m,他立即确定池塘两端A、B两点的距离为15m.
小刚同学测量的结果正确吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:我们都知道,![]()
于是,-2x2+40x+5
=-2(x2-20x)+5
=-2(x2-20x+100)+200+5
=-2(x-10)2+205
又因为![]() ,所以
,所以![]() ,
,![]()
所以,-2x2+40x+5有最大值205.
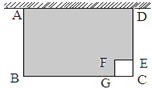
如图,某农户准备用长34米的铁栅栏围成一边靠墙的长方形羊圈ABCD和一个边长为1米的正方形狗屋CEFG.设AB=x米.
(1)请用含x的代数式表示BC的长(直接写答案);
(2)设山羊活动范围即图中阴影部分的面积为S,试用含x的代数式表示S,并计算当x=5时S的值;
(3)试求出山羊活动范围面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M,
(1)求证:M是BE的中点.
(2)若CD=1,DE=![]() ,求△ABD的周长.
,求△ABD的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织一项公益知识竞赛,比赛规定:每个班级由2名男生、2名女生及1名班主任老师组成代表队.但参赛时,每班只能有3名队员上场参赛,班主任老师必须参加,另外2名队员分别在2名男生和2名女生中各随机抽出1名.初三(1)班由甲、乙2名男生和丙、丁2名女生及1名班主任组成了代表队,求恰好抽到由男生甲、女生丙和这位班主任一起上场参赛的概率.(请用“画树状图”或“列表”或“列举”等方法给出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一条笔直公路BD的正上方A处有一探测仪,AD=24m,∠D=90°,一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°.
(Ⅰ)求B,C两点间的距离(结果精确到1m);
(Ⅱ)若规定该路段的速度不得超过15m/s,判断此轿车是否超速.
参考数据:tan31°≈0.6,tan50°≈1.2.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com