
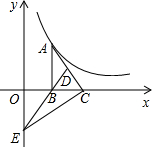
 如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC边上的中线BD的反向延长线交y轴负半轴于点E,双曲线$y=\frac{k}{x}({x>0})$的图象经过点A,若S△BEC=3,则k等于( )
如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC边上的中线BD的反向延长线交y轴负半轴于点E,双曲线$y=\frac{k}{x}({x>0})$的图象经过点A,若S△BEC=3,则k等于( )| A. | 12 | B. | 6 | C. | 3 | D. | 2 |
分析 先根据题意证明△BOE∽△CBA,根据相似比及面积公式得出BO×AB的值即为|k|的值,再由函数所在的象限确定k的值.
解答 解:∵BD为Rt△ABC的斜边AC上的中线,
∴BD=DC,∠DBC=∠ACB,
又∵∠DBC=∠EBO,
∴∠EBO=∠ACB,
又∵∠BOE=∠CBA=90°,
∴△BOE∽△CBA,
∴$\frac{OB}{BC}$=$\frac{OE}{AB}$,即BC×OE=BO×AB.
又∵S△BEC=3,
∴$\frac{1}{2}$BC•EO=3,
即BC×OE=6=BO×AB=|k|.
又∵反比例函数图象在第一象限,k>0.
∴k等于6.
故选B.
点评 本题考查的是反比例函数综合题,此题主要涉及到反比例函数y=$\frac{k}{x}$中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=$\frac{1}{2}$|k|.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
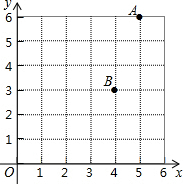 如图是某市两个小区的大致位置示意图,图中点A表示的是茗茗家所居住的小区,点B表示的是茗茗奶奶家所居住的小区,按照先列后行的顺序,点A和点B所在的位置可以表示为( )
如图是某市两个小区的大致位置示意图,图中点A表示的是茗茗家所居住的小区,点B表示的是茗茗奶奶家所居住的小区,按照先列后行的顺序,点A和点B所在的位置可以表示为( )| A. | (6,5)和(3,4) | B. | (5,6)和(3,4) | C. | (6,5)和(4,3) | D. | (5,6)和(4,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com