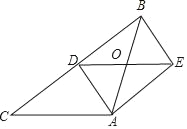
【题目】如图，D，E分别是△ABC的边AB，BC上的点，AB＝3BD，BE＝CE．设△ADF的面积为S1，△CEF的面积为S2，若
，则S1-S2的值为_____．
【答案】1
【解析】
根据S△ADF-S△CEF=S△ABE-S△BCD，所以求出三角形ABE的面积和三角形BCD的面积即可，因为AB＝3BD，所以AD=2BD，因为BE=CE，且S△ABC=6，就可以求出三角形ABE的面积和三角形BCD的面积．
解：∵BE=CE，
∴BE=
BC，
∵S△ABC=6，
∴S△ABE=S△ABC=×6=3．
∵AB＝3BD
所以AD=2BD，
因为S△ABC=6，
∴S△BCD=
S△ABC=×6=2，
∵S△ABE-S△BCD=（S△ADF+S四边形BEFD）-（S△CEF+S四边形BEFD）=S△ADF-S△CEF，
即S△ADF-S△CEF=S△ABE-S△BCD=3-2=1．
故答案为：1
步步高达标卷系列答案科目：初中数学 来源： 题型：
【题目】函数y=
是反比例函数．
（1）求m的值；
（2）指出该函数图象所在的象限，在每个象限内，y随x的增大如何变化？
（3）判断点（
，2）是否在这个函数的图象上．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知CB是⊙O的弦，CD是⊙O的直径，点A为CD延长线上一点，BC=AB，∠CAB=30°．
（1）求证:AB是⊙O的切线；（2）若⊙O的半径为2，求
的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有A、B两个港口，水由A流向B，水流的速度是4千米/小时，甲、乙两船同时由A顺流驶向B，各自不停地在A、B之间往返航行，甲在静水中的速度是28千米/小时，乙在静水中的速度是20千米/小时．
设甲行驶的时间为t小时，甲船距B港口的距离为S1千米，乙船距B港口的距离为S2千米，如图为S1（千米）和t（小时）函数关系的部分图象．
（1）A、B两港口距离是_____千米．
（2）在图中画出乙船从出发到第一次返回A港口这段时间内，S2（千米）和t（小时）的函数关系的图象．
（3）求甲、乙两船第二次（不算开始时甲、乙在A处的那一次）相遇点M位于A、B港口的什么位置？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点B，C分别在线段NM，NA上，在△ABC中，∠A∶∠ABC∶∠BCA＝3∶5∶10，且△ABC≌△MNC，则∠BCM∶∠NBA等于( )
A.1∶2B.1∶3C.1∶4D.1∶5
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，AD是BC边的中线，过点A作BC的平行线，过点B作AD的平行线，两线交于点E．
（1）求证：四边形ADBE是矩形；
（2）连结DE，交AB与点O，若BC=8，AO=
，求△ABC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，在△ABC中，∠BAC=130°，AB的垂直平分线ME交BC于点M，交AB于点E，AC的垂直平分线NF交BC于点N，交AC于点F，则∠MAN为（ ）
A.80°B.70°C.60°D.50°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
