
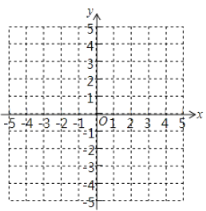
【题目】如图所示,在平面直角坐标系xOy中,△ABC的顶点坐标分别是A(-2,3),B(m-1,1),C(1,-2),点B关于x轴的对称点P的坐标为(-3,n-2).
(1)求m,n的值;
(2)画出△ABC,并求出它的面积;
(3)画出与△ABC关于y轴成轴对称的图形△A1B1C1,并写出△A1B1C1,各个顶点的坐标.
【答案】(1)m=-2,n=1;(2)画图见解析,S△ABC=![]() ;(3)画图见解析;A1(2,3),B1(3,1),C1(-1,-2).
;(3)画图见解析;A1(2,3),B1(3,1),C1(-1,-2).
【解析】
(1)根据关于x轴对称的点的坐标特征:横坐标不变,纵坐标互为相反数列方程即可求出m、n的值;
(2)根据A、B、C三点坐标即可画出图形;利用△ABC所在长方形的面积减去三个三角形的面积即可得答案;
(3)根据关于y轴对称的点的坐标特征:纵坐标不变,横坐标互为相反数即可得出A1、B1、C1的坐标,顺次连接三点即可得△A1B1C1.
(1)∵点B关于x轴的对称点P的坐标为(-3,n-2),B(m-1,1),
∴m-1=-3,n-2=-1,
解得:m=-2,n=1.
(2)∵m=-2,
∴B(-3,1)
∴如图,△ABC即为所求,
∵A(-2,3),B(-3,1),C(1,-2),
∴S△ABC=4×5-![]() ×2×1-
×2×1-![]() ×3×4-
×3×4-![]() ×3×5=
×3×5=![]() .
.
(3)∵△ABC与△A1B1C1关于y轴对称,
∴A1(2,3),B1(3,1),C1(-1,-2),
∴△A1B1C1即为所求.


科目:初中数学 来源: 题型:
【题目】(问题解决)
一节数学课上,老师提出了这样一个问题:如图1,点P是正方形ABCD内一点,PA=1,PB=2,PC=3.你能求出∠APB的度数吗?
小明通过观察、分析、思考,形成了如下思路:
思路一:将△BPC绕点B逆时针旋转90°,得到△BP′A,连接PP′,求出∠APB的度数;
思路二:将△APB绕点B顺时针旋转90°,得到△CP'B,连接PP′,求出∠APB的度数.
请参考小明的思路,任选一种写出完整的解答过程.
(类比探究)
如图2,若点P是正方形ABCD外一点,PA=3,PB=1,PC=![]() ,求∠APB的度数.
,求∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小学学生较多,为了便于学生尽快就餐,师生约定:早餐一人一份,一份两样,一样一个,食堂师傅在窗口随机发放(发放的食品价格一样),食堂在某天早餐提供了猪肉包、面包、鸡蛋、油饼四样食品.
(1)按约定,“小李同学在该天早餐得到两个油饼”是 事件;(可能,必然,不可能)
(2)请用列表或树状图的方法,求出小张同学该天早餐刚好得到猪肉包和油饼的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
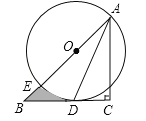
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.
(1)求证:AD平分∠BAC;
(2)若CD=1,求图中阴影部分的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
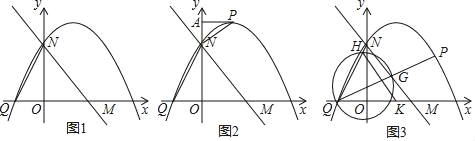
【题目】已知在平面直角坐标系xOy中,O是坐标原点,如图1,直角三角板△MON中,OM=ON=![]() ,OQ=1,直线l过点N和点N,抛物线y=ax2+
,OQ=1,直线l过点N和点N,抛物线y=ax2+![]() x+c过点Q和点N.
x+c过点Q和点N.
(1)求出该抛物线的解析式;
(2)已知点P是抛物线y=ax2+![]() x+c上的一个动点.
x+c上的一个动点.
①初步尝试
若点P在y轴右侧的该抛物线上,如图2,过点P作PA⊥y轴于点A,问:是否存在点P,使得以N、P、A为顶点的三角形与△ONQ相似.若存在,求出点P的坐标,若不存在,请说明理由;
②深入探究
若点P在第一象限的该抛物线上,如图3,连结PQ,与直线MN交于点G,以QG为直径的圆交QN于点H,交x轴于点R,连结HR,求线段HR的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(k﹣5)x+1﹣k=0(其中k为常数).
(1)求证无论k为何值,方程总有两个不相等实数根;
(2)已知函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,求k的取值范围;
(3)若原方程的一个根大于3,另一个根小于3,求k的最大整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
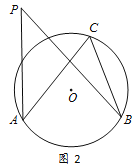
【题目】如图1,点A、B、C分别是⊙O上不重合的三点,连接AC、BC.
(1)如图2,点P是直线AB上方且在⊙O外的任意一点, 连接AP、BP.试比较∠APB与∠ACB的大小关系,并说明理由;
(2) 若点P是⊙O内任意一点, 连接AP、BP,比较∠APB与∠ACB大小关系;
(3)如图3,在平面直角坐标系xOy中,点A与点B的坐标分别是(1,0),(5,0),点P是直线y=-x上一动点,当∠APB取得最大值时,直接写出点P的坐标,并简要说明点P的位置是如何确定的.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商贸公司有![]() 、
、![]() 两种型号的商品需运出,这两种商品的体积和质量分别如下表所示:
两种型号的商品需运出,这两种商品的体积和质量分别如下表所示:
体积(立方米/件) | 质量(吨/件) | |
| 0.8 | 0.5 |
| 2 | 1 |
(1)已知一批商品有![]() 、
、![]() 两种型号,体积一共是20立方米,质量一共是10.5吨,求
两种型号,体积一共是20立方米,质量一共是10.5吨,求![]() 、
、![]() 两种型号商品各有几件?
两种型号商品各有几件?
(2)物资公司现有可供使用的货车每辆额定载重3.5吨,容积为6立方米,其收费方式有以下两种:
①按车收费:每辆车运输货物到目的地收费600元;
②按吨收费:每吨货物运输到目的地收费200元.
现要将(1)中商品一次或分批运输到目的地,如果两种收费方式可混合使用,商贸公司应如何选择运送、付费方式,使其所花运费最少,最少运费是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com