Question

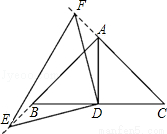
如图，在△ABC中，∠BAC＝90°，AB＝AC＝6，D为BC的中点．

（1）若E、F分别是AB、AC上的点，且AE＝CF，求证：△AED≌△CFD；

（2）当点F、E分别从C、A两点同时出发，以每秒1个单位长度的速度沿CA、AB运动，到点A、B时停止；设△DEF的面积为y，F点运动的时间为x，求y与x的函数关系式；

（3）在（2）的条件下，点F、E分别沿CA、AB的延长线继续运动，求此时y与x的函数关系式．

 

Answer 1

（1）证明见试题解析；（2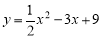）；（3）．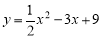

【解析】

试题分析：（1）利用等腰直角三角形的性质得到∠BAD=∠DAC=∠B=∠C=45°，进而得到AD=BD=DC，为证明△AED≌△CFD提供了重要的条件；

（2）利用S四边形AEDF=S△AED+S△ADF=S△CFD+S△ADF=S△ADC=9 即可得到y与x之间的函数关系式；

（3）依题意有：AF=BE=x﹣6，AD=DB，∠ABD=∠DAC=45°得到∠DAF=∠DBE=135°，从而得到△ADF≌△BDE，利用全等三角形面积相等得到S△ADF=S△BDE从而得到S△EDF=S△EAF+S△ADB即可确定两个变量之间的函数关系式．

试题解析：（1）∵∠BAC=90° AB=AC=6，D为BC中点∴∠BAD=∠DAC=∠B=∠C=45°，

∴AD=BD=DC，

∵AE=CF∴△AED≌△CFD（SAS）

（2）依题意有：FC=AE=x，

∵△AED≌△CFD，∴S四边形AEDF=S△AED+S△ADF=S△CFD+S△ADF=S△ADC=9，

∴，

∴；

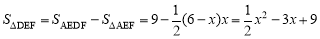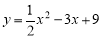（3）依题意有：AF=BE=x﹣6，AD=DB，∠ABD=∠DAC=45°，∴∠DAF=∠DBE=135° ，

∴△ADF≌△BDE，∴S△ADF=S△BDE，∴S△EDF=S△EAF+S△ADB=，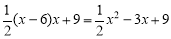

∴．

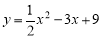考点：1．等腰直角三角形；2．全等三角形的判定与性质．