
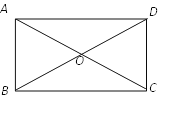
【题目】矩形ABCD的对角线相交于点O,AC=![]() ,CD=1,
,CD=1,
(1)尺规作图:作∠ABC的平分线交AD于点E,连结CE;
(2)判断线段BE与CE的关系,并证明你的判断.
【答案】(1)作图见解析(2) 证明见解析
【解析】试题分析:(1)根据基本作图——作角的平分线即可;
(2)先根据勾股定理求出AD的长,然后根据角平分线的性质(角平分线上的点到角的两边的距离相等)和判定(到角的两边距离相等的点在角的平分线上)证出BE=CE.
试题解析:(1)如图所示
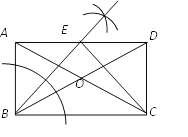
(2) BE⊥CE且BE=CE 理由如下:
∵矩形ABCD中,
∴∠BAD=∠ADC =∠ABC= 90°,AB=CD,AD∥BC.
∴在Rt△ADH中,AC=![]() ,CD=1,
,CD=1,
∴![]()
∵BE平分∠ABC
∴∠ABE=∠EBC= 45°
∵AD∥BC
∴∠AEB=∠EBC
∴∠AEB=∠ABE= 45°
∴AB=AE
∵AB=CD
∴AE=AB=1,DE=AD-AE=1
∴AE=DE
∴△DAB≌△DEB(SAS),
∴BE=CE且∠CED=∠AEB= 45°.
∴∠BED=180°-∠AEB-∠CED = 90°
∴BE⊥CE且BE=CE


科目:初中数学 来源: 题型:
【题目】某人将一枚质量均匀的硬币连续抛10次,落地后正面朝上6次,反面朝上4次,下列说法正确的是( )
A.出现正面的频率是6
B.出现正面的频率是60%
C.出现正面的频率是4
D.出现正面的频率是40%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=![]() ,点D在BC延长线上,连接AD,过B作BE⊥AD,垂足为E,交AC于点F,连接CE.
,点D在BC延长线上,连接AD,过B作BE⊥AD,垂足为E,交AC于点F,连接CE.
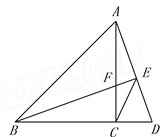
(1)求证: CF=CD;
(2)求证: ![]() ;
;
(3)探究线段AE,BE,CE之间满足的等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解七年级同学对三种元旦活动方案的意见,校学生会对七年级全体同学进行了一次调查(每人至多赞成一种方案).结果有115人赞成方案1,62人赞成方案2,40人赞成方案3,8人弃权,请用扇形图描述这些数据,并对校学生会采用的哪种方案组织元旦活动提出建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′E的长为( )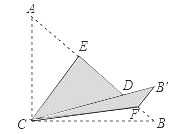
A.![]()
B.6
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com